Russell J. Donnelly
541-346-4226 (Tel)
541-346-5861 (Fax)
|
<<Previous | Page1 | Page2 | Page3 | Page4 | Page5 | Page6 | Page7 | Next>> | |
Table
1 : : 2 : : 3
: : 4 : : 5
Saturated Vapor Pressure
The
Calculated Thermodynamic Properties of Superfluid Helium-4
James S. Brooks and Russell J. Donnelly
3.1.c. The Roton Minimum
The region of the spectrum denoted (c) in figure 1 is called the "roton minimum" and can be very well represented by Landau's parabolic expression
ronton=
+
( p-po)2/2u
where is the minimum roton energy, or energy gap, p0 is the roton momentum
at minimum energy, and ??is the effective mass of excitation near p0.
These three quantities which describe the roton minimum are called the
"Landau parameters", and have the typical values at 1.I K, SVP
of /k
= 8.68 K,
po/
=
1.91Å-1, and 
. The temperature,
pressure, and density dependence of these parameters are best known from
the experimental work of Dietrich et al. [3], who find that and 
decrease
with increasing temperature and/or pressure, but that p0
is a function of density only:
po/
=3.64p1/3A-1
Values
of eq (6) are given in table 24.
Donnelly [15] has provided simple relations for the density dependence
of
and at
T = 0, and also for the relation between
and at finite
temperatures:
(p,0)/k=(16.99-57.31p)(K)
u(p,0)=(0.32-1.103p)(m)
An
expression which describes the temperature and density dependence of(,T)/k has
been given by Brooks and Donnelly [16]:
where
is the
normal fluid density and Nr
is the roton number density (both quantities will be discussed in section
4). Here, a =8.75
X 10-23 cm3 K. Equation (10) gives a
good qualitative description of the data of Dietrich et al. [3] to within
20% for [and through
eq (9)] below the lambda point. These expressions are discussed in detail
by Brooks [18].
Recently, motivated by (10), we have performed a least squares fit on
the data for, and
, using
expressions of the form
(p,T)/k
= 1+
2+
3et
T/p+ 4e2t
P and
u(p,T)=U1+
U2et T +
U3p +
U4et
T + (U5
+ U6p)
e3t (m)
Here,t = -(p,0)/kT,
and the coefficients of eqs (11) and (12) are:
=17.4167 (K)
2= -60.48823
(K g-1 cm3)
3
= -0.5307478 (g cm-3)
4
= 1.81726 X 104
(K g-1 cm3)
5
= -1.351398 X 107 (K)
6
= 1.621499 X 108 (K
g-1 cm3)
7=
-5.062661 X 108 (K
g-2 cm6)
and
U2 = 1.239037 (m K-1)
U3 = -1.238153 (m g-1 cm3)
U4 = -0.2234561 (m K-1 g cm-3)
U5 = -13429.95 (m)
U6 =632197.06 (m g-1 cm3)
The experimental roton energy gap and effective mass are shown in figures 5 and 6 with the results of eqs (11) and (12) respectively. Although eqs (11) and (12) suggest an expansion in terms of the roton number density, no particular theoretical significance can be attached to the terms in these equations. We will see in section 3.1.f below that the experimental values of and described in this section will have to be adjusted slightly to obtain the accurate thermodynamic information from the Landau theory.
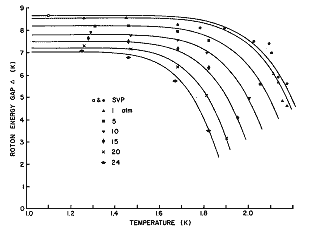
Figure 5. Least squares fit
of eq (11) to the experimental roton energy gap . Data at SVP, Henshaw
and Woods [5] (solid circles), Cowley and Woods [2] (open circle); data
at higher pressures, Dietrich et al. [3].
Figure
6. Least squares fit of eq (12) to the experimental roton effective mass
. Data point at SVP, Cowley and Woods [2]: data at higher pressures, Dietrich
et al. [3].
3.1d. The Shoulder beyond the Roton Minimum
Recent
neutron scattering experimental results (Graf, Minkiewicz, Møller,
and Passell [6] indicate that for momenta larger than po/the
slope of the spectrum approaches the velocity of sound at a momentum
, as shown
at point (d) in figure 1 and by he arrow in figure 3. The spectrum then
bends over and approaches twice the roton energy (curve B in figure 1),
finally terminating at a momentum p'. The experimental spectrum in figure
3 also has this qualitative feature. This behavior for large momenta was
predicted by Pitaevskii [29] to be
p(p)=2-
exp[-/(p'-p)]
where
and a are constants to be determined. Neutron measurements
have not yet been made over a sufficient range to provide information
for the dependence of eq (13), and in particular and a, on temperature and pressure. Fortunately, like the
maxon peak, this region of the spectrum has little thermodynamic content,
and it is sufficient for our purposes to locate the momentum pc
to the right of p0
at which 
from eq (5) reaches the slope of the velocity of first sound u1,
and to represent the dispersion curve as a straight line of slope u1 above pc, terminating at 
.
This is curve C in figure 1, which is given by
(p)=u1(p-pe)
+ (pe)p
pe
where
Pe=
u1
+p0.
This
approximation is also indicated in figure 3 as the straight line above
pe/ 
3.1.e. A Polynomial Representation for the Excitation Spectrum
We
may summarize the behavior of the excitation spectrum described in the
previous sections in the following way:
The excitation spectrum starts out at zero momentum and energy with the
slope . Hence
(0)=0;'(0)=u1
at
point (a) of figure 1. Here'
(p)=d(p)/dp
. For momentum increasing from zero, the spectrum attains its first maximum
at 1.1Å-1,
and
(1.1Å-1)=max;
(1.1Å-1)=0,
at point (b) in figure 1. Continuing down to the roton minimum, we find that the parabolic representation near po provides us with the relations
(p0)=;'
(p0)=0;''
(p0)=1/;
at point (c) of figure 1. Beyond the roton minimum, for momentum pc where the slope approaches the velocity at sound, we finally have
'
(pe)=u1
at
point (d) in figure 1.
Clearly, eqs (16) through (19) represent the most important features of
the excitation spectrum. We have discovered, partially guided by theoretical
considerations (see Feenberg [27]), that a polynomial in momentum without
a quadratic term
(p)/k=
u1P + 3P3
+ 4P4+
5P5
+ 6P6
+ 7P7
+ 8P8,
is
an excellent representation for the excitation spectrum in the momentum
interval 
and
that by using eq (14) for the interval pe/
p/
3.0Å-1
, one has a continuous expression for the spectrum which may be used to
great advantage in the computation of thermodynamic properties based upon
the Landau theory. Note that if eq (20) is continued above pc
it diverges negatively, as indicated by the dotted line in figure 1. Hence
care must be used to apply eq (14) above pc
The
coefficients an
of eq (20) may be obtained for any temperature and pressure by applying
the conditions imposed by eqs (16) through (19), which in turn will depend
on T and P. Since there is no constant term, and the
first coefficient must be u1,
the problem of determining the coefficients an
is reduced to solving six equations with six unknowns, at any temperature
and pressure.
The degree to which eqs (20) and (14) fit the neutron scattering data
is. shown as the solid line in figure 3 at 1.1 K, SVP, and again by the
solid lines in figure 7 at 1.1 K, at SVP, and at 25.3 atm. The experimental
values were used in eqs (16) through (19) to obtain these plots. One can
appreciate. from figure 7 how the spectrum changes with pressure.
.
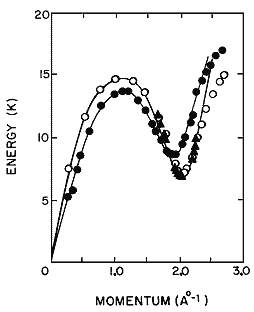
Figure 7. The excitation spectrum at two pressures at 1.1 K. Dots, SVP, open circles, 25.3 atm, Henshaw and Woods [4]; triangles, 1.25 K, 24.26 atm, Dietrich et al.[3]; solid lines, eqs (20) and (14).
As mentioned in section 3.1.a, a controversy surrounds the exact form that eq (20) should have for small momenta. We make here several comments concerning our choice of eq (20). First, we found that a series with no quadratic term was by far the best fit to the neutron data. A detailed comparison of several series is given by Brooks [18]. Secondly, one can see by inspection of the results of such calculations that the coefficient of the first nonlinear term a3 changes sign upon increasing pressure. We find this to be consistent with the results of Phillips et al. [28] (see Brooks and Donnelly [17]). Finally, the form of eq (20) has prompted us to make some calculations concerning the low temperature behavior of the second sound velocity (Brooks and Donnelly [30]). The second sound velocity is quite sensitive to the leading terms in (20) and a careful measurement would serve as a check on the form we have chosen [30].
|
