



Russell J. Donnelly
541-346-4226 (Tel)
541-346-5861 (Fax)

![]() Taylor
Vortex Flow
Taylor
Vortex Flow
The
Couette-Taylor problem concerns flow between independently rotating cylinders.
It is a widely studied example of a system removed from equilibrium, in
which the nonequilibrium condition is achieved by inducing mechanical
stresses on the fluid through motion of the cylinder walls. The system,
originally designed independently by Couette (1888) and Mallock (1888)
for investigation of the viscous behavior of fluids, was the subject of
a landmark work by G. 1. Taylor (1923). In his study, Taylor quantitatively
predicted and experimentally confirmed the existence of a flow instability
when the inner cylinder reaches a critical speed. For low cylinder speeds,
the fluid simply moves azimuthally around the cylinders. Taylor observed
that when this simple flow becomes unstable, it is replaced by a cellular
pattern in which the fluid travels in helical paths around the cylinders
in layers of vortices-now known as Taylor vortices (figs. 2,3).
Flow between rotating cylinders is remarkable for the fact that slow increase
of the speed of the inner cylinder gives rise to a progression of clearly
distinguishable fluid states that have increasing complexity. A series
of transitions occurs in steps that may be arrested and studied independently,
starting with the simplest, featureless flow and ending with fine-scale
turbulence. This is to be contrasted with other fluid experiments, such
as flow in boundary layers or between parallel plates, where turbulence
arises-beyond a relatively low critical rate of flow- in a downstream
spatial development of complexity. In such flows it is considerably more
difficult to identify distinct stages of instability and transition.
A vivid illustration of the variety of flow patterns achieved in the Couette-Taylor
system is the diagram from Anderek, Liu, and Swinney ( 1986) identifying
flow states obtained by systematic variation of inner and outer cylinder
speeds. A collection of excellent photographs of the various flow patterns
may be found in the paper by Andereck et al. The boundaries separating
the flow states depend, in many cases, on the exact protocol used in varying
the parameters. This is an important signature of nonlinearity in fluid
flow problems: the flow state depends on the history of its preparation.
This was clearly established in an important paper by Coles (1965).
The sequence of transitions is also sensitive to the geometry, and in
particular to the ratio of inner and outer cylinder radii. Andereck's
diagram was produced for a radius ratio of 0.883. Surveys at other radius
ratios, accompanied by sketches of the flow patterns in a cross-section
of the gap between the cylinders, may be found in Snyder (1970). Such
surveys have been done with relatively long cylinders, and the theory
for such systems often assumes the length is infinite. In contrast, experiments
can be done in short cylinders, where the length of the system becomes
an additional parameter: see the reviews by Mullin (1991, 1993).
The Couette-Taylor problem is also characterized by experiments of very
high precision. In this way, it is comparable to the problem of a horizontal
layer of fluid subject to a destabilizing temperature gradient (the Rayleigh-Bénard
problem). In many respects the Couette-Taylor problem is simpler because
the flow starts out clearly anisotropic in the three principal directions
(radial, azimuthal, and axial). This means there is less ambiguity about
the kind of patterns that can form in the early stages of transition.
Finally, the Couette-Taylor experiment is usually a closed system, meaning
that no fluid flows into or out of it. However, this is not always the
case, and experiments with flow in the axial direction have been carried
out.
Tagg (1992) created a bibliography of papers in this subject about 1992
and found more than 1500 references! Remarking on the tremendous number
of variants on this problem, Tagg called Couette-Taylor flow the “hydrogen
atom” of fluid mechanics.
"Taylor-Couette Flow: The Early Days", R. J. Donnelly. Physics Today, November 1991: 32-39 (1991),
and the progression of instrumentation is described in:
"Evolution of Instrumentation for Taylor-Couette Flow" R. J. Donnelly. Ordered and Turbulent Patterns in Taylor-Couette Flows. C. D. Andereck and F. Hayot, Eds. New York, Plenum Press: 1-27.(1992).
Taylor-Couette flow of helium II
Taylor Couette flow has many variants. The first problem attempted by the Donnelly group was to see if the linear stability theory for the classical Taylor vortex problem could be made to work for the two-fluid theory of helium II. The importance of this problem is that the celebrated Taylor analysis settled the case for the validity of the Navier Stokes equation and the boundary conditions. The first attempt was by Chandrasekhar and Donnelly, but who got it wrong because the form of the equations of motion (called HVBK today) was still up in the air, and they neglected the term in vortex tension.
"The Hydrodynamic Stability of Helium II Between Rotating Cylinders, I", S. Chandrasekhar and R. J. Donnelly. Proc. Roy. Soc. A214: 9-28 (1958)
The first experiments on this subject were done by Donnelly in an early PRL:
"Experiments on the Hydrodynamic Stability of Helium II Between Rotating Cylinders", R. J. Donnelly. Phys. Rev. Lett. 3: 507-508 (1959).
The apparatus (at the University of Chicago) is shown below.
![]()


![]()
"Flow and Stability of Helium II Between Concentric Cylinders", R. J. Donnelly and M. M. LaMar.J. Fluid. Mech.(1988).
The challenge was taken up by C. A. Jones and C. F. Barenghi who produced a very complete set of predictions. We decided to look for their predictions using second sound, and the results formed Chris Swanson’s PhD thesis, and appeared in
"Instability of Taylor-Couette Flow of Helium II", C. J. Swanson and R. J. Donnelly. Phys. Rev. Lett. 67: 1578-1581 (1991).
This experiment is the first instance of success of a linear instability theory with modern equations of motion for helium II and shows that the equations and boundary conditions used in the analysis are correct. This most recent version of the equations of motion is due to Hills and Roberts.
Torque measurements in Taylor-Couette flow
The apparatus shown above made it easy to do useful experiments in room temperature fluids as well. These were done and summarized in a review article:
"An Empirical Torque Relation for
Supercritical Flow Between Rotating Cylinders", R. J. Donnelly and
N. J. Simon. J. Fluid. Mech. 7(Pt. 3): 401-418 (1960).
These results were particularly useful for mathematicians (particularly
J. T. Stuart and his students) studying the nonlinear instability theory
which predicts the torque past the onset of instability. Recently Henderson
and Barenghi (Physics Letters A 191, 438 (1994) have been able to do the
nonlinear theory of torque in helium II to account quantitatively for
Donnelly’s 1959 torque measurements in helium II.
Chandrasekhar also worked on the stability of hydromagnetic flows, in particular Taylor-Couette flow of a conducting fluid in a magnetic field (see Chandra’s remarkable book Hydrodynamic and Hydromagnetic Stability, Oxford, 1961). Our group undertook to verify these calculations using the hydromagnetic Couette viscometer shown below, with magnetic field furnished by an old cyclotron magnet.
![]()

The results were published in 1962:
"Experiments on the Stability of Flow Between Rotating Cylinders in the Presence of a Magnetic Field", R. J. Donnelly and M. Ozima. Proc. Roy. Soc. A266: 272-286 (1962).
The
experiment in place is shown below. This cyclotron now sits beside the
entrance drive to Fermilab.
![]()

In the days before techniques such as LDV and PIV were invented, there was no quantitative way to see the Taylor vortices. We therefore devised an electrochemical technique which allowed direct observation of the vortex array:
"Experiments on the Stability of Viscous Flow Between Rotating Cylinders IV. The Ion Technique", R. J. Donnelly. Proc. Roy. Soc. A283: 509-519 (1965).
The principal of obtaining scans of the vortex patterns is shown below:
![]()

This
technique allowed Donnelly and Schwarz to verify the “Landau Law”
for the growth of equilibrium amplitude of vortex motion above critical:
![]()
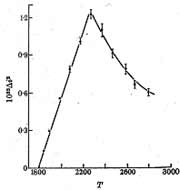
and to study in detail the transient response to a sudden transition through
the critical speed:
![]()
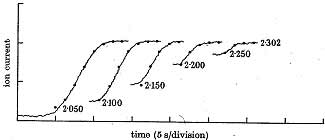
"Experiments on the Stability of Viscous Flow Between Rotating Cylinders
VI. Finite Amplitude Experiments", R. J. Donnelly and K. W. Schwarz. Proc.
Roy. Soc. A283: 531-556 (1965). The relevant theory is discussed in Chapter
3 of Landau and Lifshitz Fluid Mechanics, Second edition
Modulated Taylor vortex flow
Acting on a suggestion by Fred Reif and Harry Suhl, we began an investigation into the stability of modulated Taylor Vortex flow. In the days before stepping motors we had to use one Graham variable speed drive to modulate the speed control of another:
![]()

"Enhancement of Hydrodynamic Stability by Modulation", R. J. Donnelly,
F. Reif and H. Suhl. Phys. Rev. Lett. 9: 363-365 (1962).
This problem lasted for many years with various twists and turns, and even was extended to Rayleigh Bénard convection. A review article summarizes the present situation briefly:
"Externally
Modulated Hydrodynamic Systems", R. J. Donnelly in. Nonlinear Evolution
of Spatio-temporal Structures in Dissipative Continuous Systems F.
Busse, ed., Streitberg (Bayreuth) Germany,1990.
Visual Studies of Taylor Couette Flow
Russell Donnelly and Dave Fultz constructed a large rotating cylinder
pair at the University of Chicago. This is shown in the photograph below
taken in 1961, with Sir Geoffrey Taylor and Dave Fultz. Many of the visual
experiments are described in Chandrasekhar’s 1961 stability book.
A photo of Chandra the day the book was received is shown below.
![]()

![]()

