<<Previous

Page1

Page2

Page3

Page4

Page5

Page6

Page7

Next>>

Table 1 : : 2 : : 3 : : 4 : : 5

The Calculated Thermodynamic Properties of Superfluid Helium-4
James S. Brooks and Russell J. Donnelly

4.3.c. The Gibbs Free Energy

The Gibbs free energy has a ground state Part _o (P) and an excitation part _E(P, T) given by the double integral in table I. _o(P) can be determined by integrating the expression d = VdP.. The results determine _o at T =0 K to within an additive constant L_o as described in section 4.3.b. above.

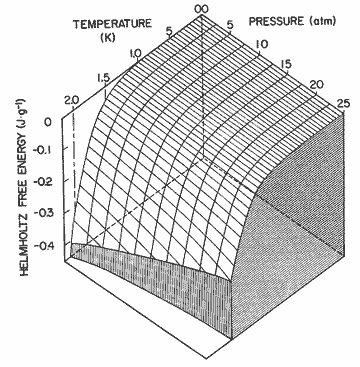
Figure 13. The Helmholtz free energy of the excitations as a function of pressure and temperature. The Gibbs free energy has substantially the same appearance.

Table V. The ground state Gibbs free energy o(P) = [(0, P) -(0,0)] J g-1
P(atm)	0	2.5	2	7.5	10	12.5
0( P )J.g-1	0	1.7205	3.3972	5.0373	6.6457	8.2263
P(atm)		15	17.5	20	22.5	25
0( P )J.g-1		9.7821	11.316	12.829	14.323	15.800

The Gibbs free energy is not directly accessible experimentally. The data of table V come from integration of the equation of state of Abraham et al. [31] and hence should be reliable. The excitation part of the Gibbs free energy is tabulated in table 7: the appearance of this energy surface is similar to the Helmholtz energy in figure 13. We have checked the integration by comparing to ( / T )p to S. The differences are less than 0.3% over most of the T-P plane and never exceed 1%.

4.3.d. The Enthalpy

The enthalpy W has a ground state part W_o (P) and an excitation part W_E (P, T) as given by the double integral in table I. The ground state part W_o (P) = _o(P) is tabulated in table V in section 4.3.c. above. The enthalpy of the excitations is tabulated in table 8 and illustrated in figure 14.

We have cross-checked our tabulations with the equivalent expression . We find the differences are less than 1.7% at most temperatures and pressures. The enthalpy, then, should have the same basic accuracy as the specific heat, as discussed in section 4.3.e below.

4.3.e. The Specific Heat

The specific heat at constant pressure,

is obtained by the integral expression in table I. Below 1 K this worked satisfactorily; above 1 K we experienced difficulty in getting a smooth table. We therefore used (29) directly, selecting five local entropy values, fitting a quadratic function by least squares, and finding from that function. The resulting values are listed in table 10 and plotted in figure 15.

The deviations C_P = (C_{P calc} - C_{P meas}) C_{P meas} have been compared with the data of Wiebes [36] for T 1.6 K.

P(atm)	0	5	10	15	20	25
%	2.2	1.5	1.4	0.88	1.0	2.0
%	6.5	3.0	2.2	2.3	3.3	2.8

The ratio of specific heats is compiled from

The term in is subject to an accumulation of errors and is perhaps as much as 50% in error in some regions. Values of ? are tabulated in table 12.

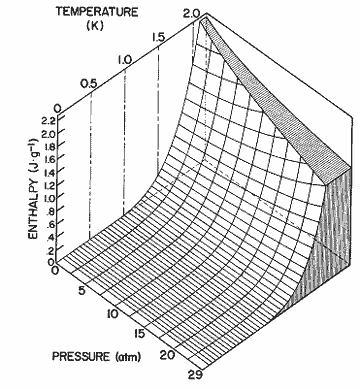
Figure 14. The enthalpy of the excitations as a function and pressure and temperature, as calculated from the expression in table I.

The specific heat at constant volume C_V = CP / is listed in table 11. Although is quite uncertain, the correction is generally small. Comparing with the data of Wiebes [36], we find the deviations are as follows (T 1.6 K):

P(atm)	0	5	10	15	20	25
%	2.2	1.6	1.4	1.0	2.2	2.7
%	6.5	2.9	2.1	2.3	3.2	2.6

Table I shows an integral expression for CV . We have used the correction of eq (30) rather than our theoretical expression because the latter involves a derivative at constant volume.

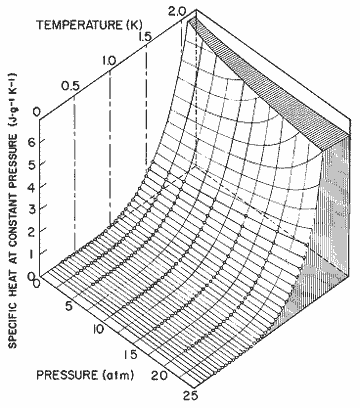
Figure 15. The specific heat at constant pressure as a function of pressure and temperature, calculated from the expression in table I. Data, Wiebes, [36].

4.4. Superfluid Properties
4.4.a. The Excitation Number Densities

The density of thermal excitations, calculated by numerical integration, has been separated into a phonon part NP and a roton part Nr by defining (quite arbitrarily) excitations with wave number less than 1.1 Å-1 phonons. For phonons, we have for the number density [from eq (1)]

and for rotons

where q_max=1.1 Å^-1 q_f =3.0 Å^-1. Tabulations of N_p and N_r appear in tables 13 and 14, respectively. No comparison of the results can be made since the number densities are not directly accessible experimentally.

4.4.b. The Normal Fluid and Superfluid Densities

The normal fluid density may be computed from Landau's expression

and the computed values appear in table 15. From the equation of state, we may obtain the superfluid density by subtraction of ,

p_s = p - p_n,

and one may also obtain the ratios p_n/p and p_s/p. The quantities p_n/p, p_s, and p_s/p appear in tables 16, 17, and 18 respectively, and p_n/p is plotted in figure 16.

The calculations can be compared with a variety of experiments. At the vapor pressure, the deviations p_n = (p_{n cale} - p_{n meas})/(p_{n meas})from the data of Tough et al. [44] are , with most of the latter error occurring at 2 K and above. Comparing with some unpublished data of Maynard (based on second and fourth sound measurements [21]), one finds the following:

P(atm)	0	5	10	15	20	25
	3.1	2.7	2.5	3.8	3.6	8.0
	0	2.8	4.0	3.5	5.8	5.0

The oscillating disk data of Romer and Duffy [45], principally above 1.6 K, averages about 4-7% low compared to our calculations.

4.4.c. The Velocity of Second Sound

The velocity of second sound, neglecting thermal expansion, is

where u_II was used to correct the velocity of first sound in section 4.2.a above. Allowing for thermal expansion the velocity of second sound is given by [40, 41].

Figure 16. The normal fluid fraction as a function of temperature for different pressures calculated from eq (33). The data points are from Maynard [21].

We have used equation (34) to compute u₂, with results given in table 19 and figure 17. The data shown in figure 17 is that of Heiserman et al. [21]. Comparison of our results with the data of [21] is as follows:

P(atm)	0	5	10	15	20	25
	0	0.5	0.1	0.6	0.9	0.8
	2.1	1.7	2.4	4.6	4.2	4.8

Below 0.8 K, the calculated values show marked effects of phonon dispersion, as discussed by Brooks and Donnelly [30].

Figure 17. The velocity of second sound as a function of temperature, at different pressures. Solid lines, eq (34); data points, from Heiserman et al. [21]. Some of the unevenness of the calculated curves may be the result of numerical problems; note how many derived quantities appear in eq (34).

4.4.d. The Velocity of Fourth Sound

The velocity of fourth sound is, to good approximation [40, 41]

We have used equation (35) to compute u4, with results given in table 20 and figure 18. The deviations, compared with the data of Heiserman et al. [21] are:

P(atm)	0	5	10	15	20	25
	0.3	0.5	0.9	6.4	1.5	1.4
	0.4	5.3	6.4	0.2	0.5	2.4

5. Conclusions

We have provided tables of the thermodynamic and superfluid properties of helium II computed, when possible, by theoretical methods. Due to inadequacies in the present theory, we were not able to achieve absolute agreement with the experimental data in all cases. The accuracy of our computed values is, however, generally very good, and we hope that the tables will provide a ready reference for theoretical and experimental research in helium II .

Perhaps the most interesting outcome of this research, other than the tables, is the result that there appears to be no theory at present which can accurately relate the energy and momentum of the elementary excitations of helium II, as measured by inelastic neutron scattering, to the thermodynamic properties. The problem may be in part the assumption of zero line width for the spectrum, but other considerations such as the time scale of the neutron probe, and the re-establishment of equilibrium after an excitation is created, may prove important factors. These tables provide a unique opportunity for comparison of the spectrum measured by neutron scattering, and the spectrum which yields the correct thermodynamic properties via the Landau theory, and it is hoped that our analysis will stimulate theoretical interest in this problem.

On the experimental side, we see that there are serious gaps and discrepancies in some of the data which have been considered established for many years. Even the equation of state would benefit from a systematic study over the entire (T, P) plane. An ideal experiment would simultaneously measure the velocities of first, second, and fourth sounds, and the expansion coefficient in one cryostat over all pressures and all temperatures from 0.3 K upward. When such data are available, the present study could be repeated with considerable profit.

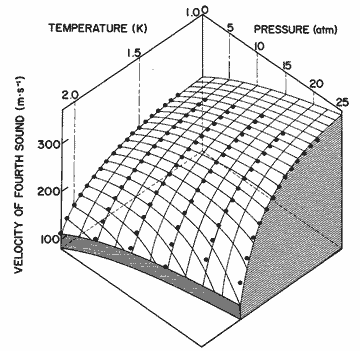
Figure 18. The velocity of fourth sound as a function of pressure and temperature calculated from eq (35). The data points are from Heiserman et al. [21].

6. Acknowledgments

This research was supported by the Air Force Office of Scientific Research under grant AFOSR-76-2880 and by the National Science Foundation under grant DMR-72-3221/A01. This work was begun when the authors were guests at the Niels Bohr Institute, Copenhagen, and we thank Professor Aage Bohr for the hospitality of the Institute. We would also like to thank Mr. James Gibbons for much help in the preparation of the computer results for our initial report, and for the entire task of preparing the present tables using recent data and the formulae of table I. We are indebted to Professors D. L. Goodstein, R. P. Feynman, R. M. Mazo, and P. H. Roberts for discussions and collaboration on the theory. Professor I. Rudnick, Dr. Jay Maynard, and Dr. C. Van Degrift have made data available to us in advance of publication. We have appreciated the support and patience of the editors and staff of this Journal in the preparation of the manuscript.

<<Previous Page1 Page2 Page3 Page4 Page5 Page6 Page7 Next>>