I. Linear vs. Circular/nonlinear causality

     Systems theories present a different way of thinking about events. Central to this thinking
is the distinction  between  linear  and circular  (or nonlinear causality).
 

•  In the case of Linear causality:
•   A --> B    A is antecedent to or causes B

•   In the case of nonlinear causality:
•  A <--> B A affects B just as B affects A,  ( i.e., circular)

   Or,  more complicated examples:

•  the rate at which [A affects B] changes as [B affects A]
• the longer A <--> B is in effect, the more both [AB] and C interact e.g.,

                    (A <--> B) <--> C

• Exponential changes are non-linear by definition

II. Nature of systems

     Systems are defined as
        "A set of consistently interacting elements,
       whereby the
       Elements are mutually interdependent, and the
       Relationships among elements are highly patterned, such that
       Changes in one element affects the status of all others."

III. Three Properties of systems

   A. ORGANIZATION

        Wholeness or totalities
        Consistencies of interactions reflect and form the organization of a system;
        Systems can be organized hierarchically
        Repetitive rules of relating are patterns of  organization
      _______________________________________________________

      We observe Mother, Father, Child,  and count who is speaking to whom over
       a 15 min. interaction.

                 Note: There are ONLY six possibilities for coding who speaks: to whom:

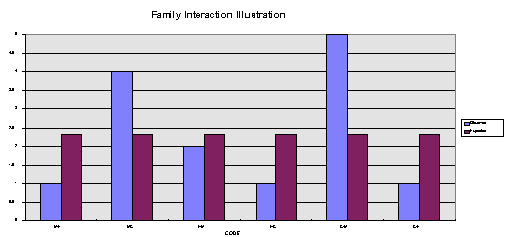
Only Possible Event Combinations

1	2	3	4	5	6
M->F	F->M	M->C	F->C	C->M	C->F

        Now here is a sample data stream (i.e., the sequence of events in real time)

          .....M-F  M-C  C-M  F-C  C-M  C-M  M-C  F-M  C-M  C-F  C-M  F-M  M-C M-C.......
                               ( = 14 separate events recorded)
 

    Notice that we only coded who was speaking to whom, not what was talked about,
   nor anything else about the family (e.g., their ages, ethnicity, personalities, etc.).

   Now tabulate the frequency of occurrence of each of the 6 event possibilities.
   Based on a random (chance) model, you would calculate the expected frequency for   each code.  Note -- "expected" here means that the 14 separate events should occur equally,  divided  among the 6 event possibilities ( i.e.,  6/14 = 2.33)

Observed          Expected

(1) M-F        2                   2.33
(2) F-M        2                   2.33
(3) M-C       ….                 2.33
(4) F-C        ….                 2.33
(5) C-M       ….                 2.33
(6) C-F        1                  2.33
              __________________
            N = 14                 13.98

    If you make a histogram, with the 6 event possibilities as the X axis, and the expected frequency
    values on the Y axis, all bars would be the same height (i.e., 2.33).

    Now if you plot the observed frequencies (maroon bars, from the table above) on the same histogram (blue bars)  you get the figure below:

     What do you notice immediately about the two sets of bars?
    How would you describe the PATTERN of interactions in this family?
    What clues does it give you as to the structure of this system?

Note: "Describe" means how it is; "explain" means how come it is.

       (A. cont'd)

          Boundaries
          Delineate separate elements of systems and subsystems
          Vary in permeability (like cell walls)
          Give examples of boundaries in families
          Hierarchies
             Systems can be organized hierarchically

Class examples from families

    B. CONTROL
         Homeostasis
         Feedback (servo mechanisms)
         Deviation amplifying -- Positive feedback
         Deviation dampening - Negative feedback

    C. ENERGY

      Entropy -- random, no pattern
      Negentropy --increased stereotypy

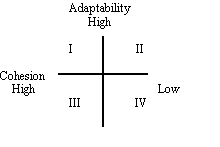
IV. Circumplex Model of Families (Figure from Lecture)

     Olson's model based on two orthogonal (right angle) vectors:
          Cohesion (X axis) and Adaptability (Y axis)
          This yields 4 quadrants of Hi and Low on each vector.

             Example:  A family can be Hi-Hi,  I;   Lo-Lo,  IV;  Hi-Lo,  III; and Lo-Hi,  II,
                                using their scores  on  these two measures (Adaptability and  Cohesion)
                                How would you describe a family that is Hi on cohesion and Lo on
                                adaptability (e.g., III)? One that  is  Lo on cohesion and Hi on
                                adaptability (e.g., II)?

 
For a view of the complete Olson model click  HERE.
   (Picure loads slowly)

V. Clinical Applications of Systems Concepts

  Communication and meta-communication
       What is wrong with this "message?"
 

All messages in this box are false


 
Double binds and paradoxes (Two ties: don't you like the other tie I bought you?)
 

Reframes and punctuating event streams           Reframes refer to taking a sequence of events that        is  otherwise negative and turning  it into something        positive.  The example from class was the affair: With       linear  thinking, affair --> bad person  With a reframe        of these  events, affair --> bringing the relationship        to a different  (hopefully better) level;  How? Now        everyone knows       there is a problem, go into therapy, seek help, etc.       Only if you assume circular causality would the        idea  of reframes even occur  to you.          What is at issue here is that any sequence of life       events can be  PUNCTUATED in different ways.       There is not just one way to look  at (punctuate) a        sequence (e.g., he does bad, she does good, he        does  more bad, she does more....) Think of things       not  coming to you in neat packages (all affairs are        bad;  all  withdrawal is bad; all asking for change is        bad)  but rather  look for another way to view the        causality.

 

Protection and balance      Given the homeostatic nature of systems, it is not  surprising that one member may take on the role of protector, or the one to draw fire.     Take sister Suzy who is anorexic. Bad thing, so family  must now focus all their attention on her. What are M  and F doing now that they are preoccupied with Suzy? For one thing, they have less chance to get into their stuff. Suzy (not planning this!) now acts as family protector by keeping M and F from fighting, etc.  Notice: Suzy did not wake up one morning saying "Oh goodie, if I starve myself I can keep  mom  and dad from fighting." No consciousness is needed  within a systems perspective! Also systems people do not rely on personality explanations. Suzy's anorexia is not a personality  disorder: it is a  solution to a problem. But...the solution IS the problem.     This is a very different way to  think of these events. What people DO to solve  "a problem"  is  often THE problem. Compare this thinking  with the psychodyanmic view. In psychodyanmic view there is an underlying  problem that is festering and must be "cut out" as it were. In  systems thinking the balance within the family  is such  that people HAVE to do whatever becomes the problem.