
| Contents of this page: | |
A more specific example of how microphotonics can make an impact is described in this PDF-article describing my field of work in the photonics industry from May 2000 until August 2001. The material system discussed there Indium Phosphide, a semiconductor compound. Other material systems for microphotonics can be found among polymers, glasses, porous media - to name a few.
At the heart of these developments is the availability of small but efficient lasers which deliver the required intense and coherent light.
|
If you have any doubts that the laser is one of
the twentieth century's most important achievements in
science and technology, please read about the impact and
history of laser light at this new website.
For an amusing but also informative glimpse of laser
physics, see the Britney Spears Guide
to Semiconductor Physics. Wikipedia is a good source of information and links on laser physics. |
As a rather logical continuation of the same principle, one has progressed to photonic crystals which employ the Bragg principle in more than one spatial direction and can in principle be used to make extremely small photonic cavities. The price one pays is that one needs many periods of the artificial crystal lattice in order to obtain high reflectivities, so that the total size of the structure ends up being much larger than the cavity itself. Higher and higher reflectivities are required, on the other hand, if one wants to make a laser out of such a microcavity. The simple reason is that a small cavity can host only a small amount of amplifying material, and therefore it becomes more difficult for amplification to win over the losses in a microcavity laser.
This is achieved with the "whispering-gallery" resonator which is at the heart of the lowest-threshold lasers made so far. This low threshold becomes possible as a consequence of the small size that can be achieved with these resonators. They are essentially circular disks in which the light circulates around close to the dielectric interface. Such modes are especially low in losses.
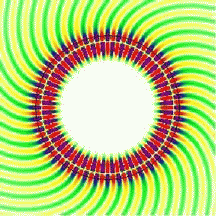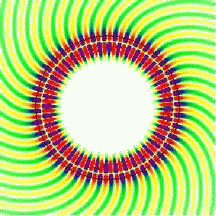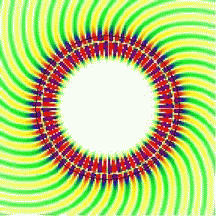
| Whispering-gallery
waves: To illustrate the whispering-gallery effect, the movie shows a cross sectional view of a curved interface (black circle) between glass and air, with a circulating wave radiating in all directions. The color represents the electric field, and in the first animation the field inside the resonator is only slightly higher than outside. This is not a good resonator because it is very "lossy". In the second movie, the wavelength is about 4 times shorter than above. In this case, the field outside the resonator is much weaker than inside it, meaning that we are confining the light much better. In both animations, the wave fronts look slanted, especially on the outside. Comparing the two clips, you will notice, however, that the wave fronts right at the circular interface are perfectly radial in the bottom image. This is what makes the two scenarios different: the straight wave fronts at the interface correspond to grazing propagation along the curved boundary. There is still a wave emanating from the cavity at the bottom, but its amplitude relative to that at the interface is now much smaller. Observe also the central region of the dielectric circle, which is essentially field-free. The intensity is highly concentrated near the surface. Even in the more strongly confined case, shown here, the wave penetrates slightly into the surrounding medium. In reflection off a straight dielectric interface, this penetration is known to go along with the Goos-Hänchen effect, a lateral displacement of the scattered beam. A calculation of the analogous effect in reflection off a curved interface can be done starting from the circular geometry. Since the Goos-Hänchen effect can be incorporated into a ray model, it improves semiclassical calculations for non-circular cavities. To find out more about the spiral patterns shown in these movies, read about wavefronts in open systems. |
 |
 |
Semiconductors are far from being the only application of the whispering-gallery mechanism. The first laser resonators in the submillimeter size regime were made of liquid droplets containing a lasing organic dye. The highest-quality optical microresonators have been achieved using fused-silica spheres (i.e., glass). Although these materials have a refractive index closer to unity than a semiconductor, they still support whispering-gallery modes. In that context, they are often called morphology-dependent resonances (MDRs).
Both the semiconductor and the droplet realizations of the whispering gallery are illustrated on the cover of
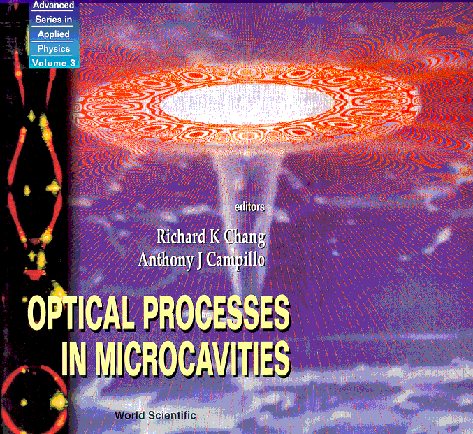
Optical Processes in Microcavities,
edited by R.K.Chang and A.J.Campillo (World Scientific
Publishers, 1996).
The lasing droplets are seen on the left side, and a
"thumbtack" microlaser with its rotationally symmetric
calculated emission pattern appears in the main panel.
The question that arises naturally in lasing microdroplets is: how strongly can a dielectric resonator be deformed before whispering-gallery modes cease to exist, or become degraded by leakage? The intuitive answer is, "the rounder, the better". However, even shapes with sharp corners can sustain modes that have every right to be called whispering-gallery phenomena. In fact, these types of whispering-gallery modes cannot be understood purely on the basis of ray optics. This is discussed in our work on hexagonal nanoporous microlasers.
Intriguingly, hexagonal zinc oxide nanocrystals have recently become the smallest resonators sustaining whispering-gallery type modes ever observed.

Being round is not a prerequisite for whispering-gallery action. So there is a huge space of possible shapes (practically from circle to square) that could possibly be considered as whispering-gallery type resonators. If we had a choice, what should the ideal shape be? This clearly depends on the application context, but in any case it would be desirable to have some design rules. In the following, we begin to discuss some design issues, and point out how our work in particular aims to provide the design rules just mentioned, based on approximate methods such as the ray picture.
If one wants to avoid the use of partially transparent
mirrors (which need to have very low losses for high-power
applications), one alternative design is the unstable
resonator containing defocussing elements [see the
exhaustive textbook by A.E.Siegman, Lasers
(University Science Books, Mill Valley, CA (1986)].
E.g., two concave mirrors separated by more than their added
radii of curvature cause rays to diverge out from the optical
axis after several reflections. Outcoupling occurs when the
light spills over the edge of one of the mirrors (which hence
need not be partially transparent themselves).
Such unstable lasers differ from stable resonators in their mode structure: A set of well-defined bound modes is not available for the expansion of the laser field, because they all couple to the outside. Therefore, it has been necessary to use quasibound states in the calculations.
Lasers are fundamentally open systems, so a description in terms of quasibound states seems only natural. These states are, however, not as familiar a tool as the usual square-integrable eigenfunctions one knows from bound systems. Their properties are still a topic of current research.
Nevertheless, their use makes a lot of sense when discussing the emission properties of individual metastable states, such as their frequency shifts as a result of a perturbation in the resonator's shape or dielectric constant.
Or - just to mention a really far-out example: metastable states find application in the study of gravitational waves emitted from a black hole [P.T.Leung et al., Phys.Rev.Lett. 78, 2894 (1997)]
Now combine this idea with the use of dielectric interfaces as (partially transparent) mirrors, and one is lead quite directly to consider the so-called stadium resonator (or a generalization thereof).
Here is an illustration of the stadium shape and of how it
scatters an incident ray:
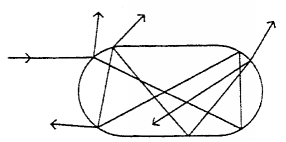
It is taken from J.H.Jensen, J.Opt.Soc.Am.A 10 (1993).
We are not the only ones to consider chaotic dielectric
resonators. However, we were the first (to my knowledge) to
seriously apply chaos analysis to the emission properties of
quasibound states in dielectric resonators, see
"Q spoiling and directionality in deformed
ring cavities",
J.U.Nöckel, A.D.Stone and R.K.Chang, Optics Letters
19, 1693 (1994).
PDF.
This is a theory paper in which we address the consequences
of emerging ray chaos for the lifetimes and emission
directionality of deformed dielectric resonators.
The first experiment in which the correspondence
between emission anisotropy and chaotic structure in the
classical ray dynamics was successfully applied to dielectric
microlasers is
"Ray chaos and Q-spoiling in lasing
droplets",
A.Mekis, J.U.Nöckel, G.Chen, A.D.Stone and R.K.Chang,
Phys.Rev.Lett. 75, 2682 (1995).
PDF.
In this paper, we studied lasing microdroplets with a
nonspherical shape, which leads to a strongly anisotropic
light output along the droplet surface. The total-intensity
profile was imaged and compared with a ray model, yielding an
explanation for the observed features.
To arrive at the idea of using a chaotic resonator cavity, one can either start from the unstable-resonator concept as described above, or from the whispering-gallery design. We came from the latter direction. The argument leading to an oval dielectric resonator is simply that a circular whispering-gallery cavity does not have a preferred emission direction, owing to its rotational symmetry. In addition, one wishes to have a parameter with which the resonance lifetimes of the cavity can be controlled. This is achieved by deforming its shape.
Microresonators such as this can find application in quantum electrodynamics because they allow to modify the rate of spontaneous emission of atoms or quantum dots interacting with the electromagnetic field. To that end, one has to go to small mode volumes. But the cavity volume isn't necessarily what counts. With a focused ray pattern as in the confocal resonator, the light field is especially strong in only certain portions of the resonator, notably the focal point in the center. And that is where the desired strong coupling between the light and the active medium occurs.
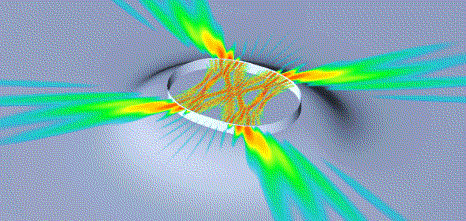
The microcylinder laser shown here is not circular, but not a stadium shape, either. The stadium has fully chaotic ray dynamics, the circle has no chaos at all. This oval shape has a mixed phase space. As a by-product of the transition to chaos which takes place with increasing deformation, a bowtie-shaped ray path is born that does not exist below a certain eccentricity. This pattern combines internal and external focussing, and its lifetime is long enough for lasing because the rays hit the surface close to the critical angle for total internal reflection.
This is the world's most powerful
microlaser to date.
To understand why this very desirable intensity distribution
arises in the smooth oval shape we chose here, but not in the
circle or the stadium, one has to use methods of classical
nonlinear dynamics. This is explained in our article,
" High power directional emission from lasers
with chaotic resonators ",
C.Gmachl, F.Capasso, E.E.Narimanov, J.U.Nöckel A.D.Stone,
J.Faist, D.Sivco and A.Cho, Science 280, 1556 (1998)
PDF, cond-mat/9806183.
This active material consists of a semiconductor heterostructure in which an electrical current leads to the emission of photons. But in contrast to more conventional quantum-well diode lasers, the optical transitions responsible for the creation of the photons take place exclusively within the nanostructured conduction band (between quantum well subbands). Electron-hole recombination across the valence band (the usual mechanism) is not involved here, leading to various advantages.
F.Capasso and J.Faist are among the winners of the 1998 Rank Prize for the invention of the quantum cascade laser.
The basic ideas of our work are illustrated on picture pages starting with a galery of magazine covers and continuing with a special type of shape called the Robnik billiard (also known as the dipole shape or limacon billiard).
How to learn more:
|
In Optics, there is a slight confusion of terminology about the concept of chaos, because it is traditionally found (in quantum optics) when people want to describe the statistical properties of a photon source. "Chaotic light" in that context has a much shallower meaning - it just means "random" thermal distribution of photons as it is found in blackbody radiation.
Chaos in the deterministic sense already has a place in optics as well, but again we have to make a distinction to our work. In multimode lasing one can look at the temporal and/or spatial evolution of the laser emission and finds that the signal can become very irregular. By mapping this behavior onto an artificial (usually many-dimensional) space, e.g. by a so-called time-delay embedding, one then sometimes finds that the system follows a trajectory on a "chaotic attractor". That's a type of structure one finds in dissipative nonlinear classical systems. This is what people have studied in nonlinear optics for a long time now.
There are many lists of chaos-science links; see for example the Wikipedia artticle on this subject. For more on the the relation between our work and the more traditional nonlinear optics, see below.
The optical resonator in the ray picture is a realization of what mathematicians call a billiard. See this short article for an entertaining introduction to billiards. Only non-chaotic billiards are shown there: the circle and the ellipse (note that this math definition of a billiard doesn't conform with what we know from the local pub). But generic oval billiards display chaotic dynamics. To take the step into the world of chaotic billiards, follow this link to the polygonal and stadium billiard (among others).
If you have any further questions about chaos, you may well find an answer at this informative FAQ site maintained by Jim Meiss. Further information, including a host of graphics and animations, is also available from the chaos group at the University of Maryland.
One of the pioneers of quantum chaos, Martin C. Gutzwiller, has written a beautiful introduction to this field in Scientific American. See in particular the third figure describing the central place of quantum chaos in our our understanding of quantum mechanics. An important lesson here is: Playing around with the simple standard systems, such as harmonic oscillators, we barely scratch the surface of what the classical-quantum transition really entails. If we want to go beyond pedestrian descriptions of this transition, classically chaotic systems are where the action is! This also holds for much-discussed fundamental topics such as "decoherence", see the example of periodically "kicked" Cesium atom. As a by-product, quantum chaos has brought together an arsenal of powerful techniques. My first chance to study these was a graduate course at Yale taught by Prof. Gutzwiller in 1993/94; he also accompanied my thesis work on chaotic optical cavities through discussions and as a reader at dissertation time.
As it turns out, many of the intrinsic emission properties of dielectric optical resonators have a classical origin. The significance of this for quantum chaos is that comparison between ray model and numerical solutions of the wave equations uncover corrections to the ray model. Alternatively, one can also discover such wave corrections by comparing the ray predictions to an actual experiment. We follow both approaches.
Such wave corrections become especially interesting when the
underlying classical dynamics is partially chaotic, as
is the case in the asymmetric dielectric resonators. In that
setting, two major new effects arise:
dynamical localization and dynamical
tunneling.
In dielectric cavities, the effect of such phenomena on resonance lifetimes and emission directionality, and of course on resonance frequencies, can be studied. Emission directionality is in itself a completely new question to investigate from the viewpoint of quantum chaos: when decay occurs, e.g.,in nuclear physics or chemistry, any anisotropy of the individual process is averaged out in the observation of an ensemble - but microlasers can be looked at individually, and from various directions. If they are bounded only by a dielectric interface, the emission pattern is determined by the phase-space structure. This is an important focus of my work: the short-wavelength asymptotics of systems that are chaotic and open.
What this means is illustrated in a slightly different example on a picture page describing the annular billiard. There, we studied the relation between resonance lifetimes and dynamical tunneling (since it involves tunneling into a chaotic portion of phase space, it is also called "chaos-assisted tunneling").
Is quantum chaos just a mathematical-conceptual game without relevance for experiments? Our work has been among the first to propose actual applications of quantum chaos phenomena, and to my knowledge the two patents I co-authored were the very first to rely on such phenomena.
What I'm discussing above is chaos in the linear wave equation. This phenomenon often dominates the physics, especially near the lasing threshold. At higher powers the nonlinearity of the medium itself becomes more important.
This is something we had earlier addressed in an invited conference contribution , and also commented on in a book chapter titled "2-d Microcavities: Theory and Experiments" .
*Note:Last significant revision: 09/09/04.This page represents a compilation of information relevant to our work on microlaser resonators. Naturally, it cannot claim to be complete in any way. However, I felt it appropriate to provide some context because the questions we are discussing are at the interface between two fields of study that traditionally haven't had much overlap: micro-optics and quantum chaos. These fields have more in common than meets
the eye. Since this is a NET DOCUMENT, I am trying to refer mostly to other documents that are available online, instead of citing things printed on dead trees. But if you have something you'd like me to include, feel free to let me know. |
This page © Copyright Jens Uwe Nöckel, 2002-2004
Last modified: Fri Oct 26 20:39:20 PDT 2018