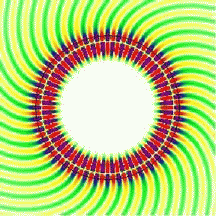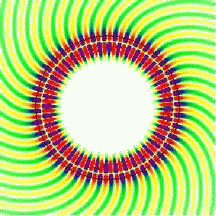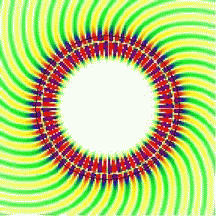
The whispering-gallery effect can lead to very efficient trapping of light in small dielectric structures. Two complementary ways of looking at this problem have given us a very good understanding of the underlying physics: rays versus waves. The linked page describes what you might call the "beginner's" version, in that it deals with ideal round shapes where light rays circle close to the boundary with perfect regularity. The resulting whispering-gallery modes look like the one shown on the right. In the ray picture, this corresponds to a ball bouncing around on a circular billiard table. The term "mode" refers to the fact that a self-sustaining wave pattern can only exist when the conditions for constructive interference inside the cavity are met.
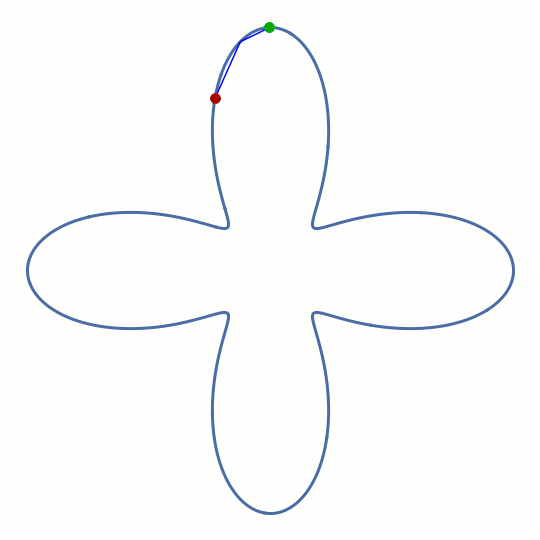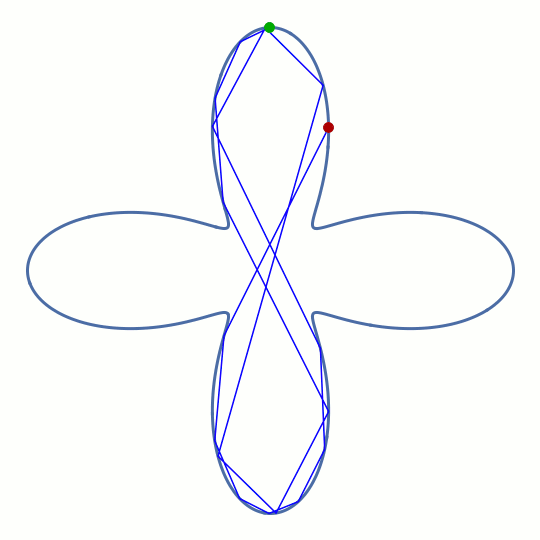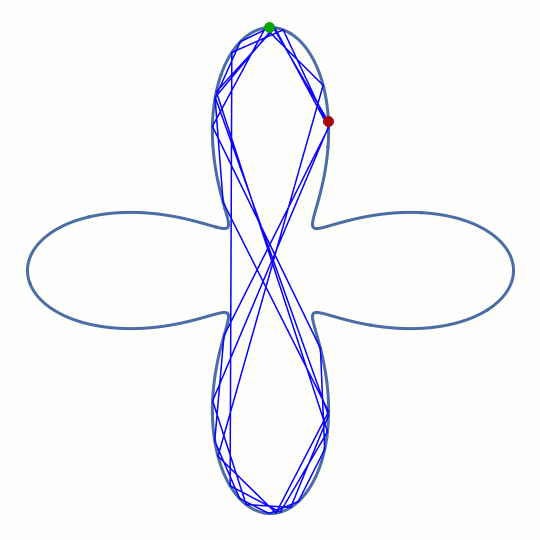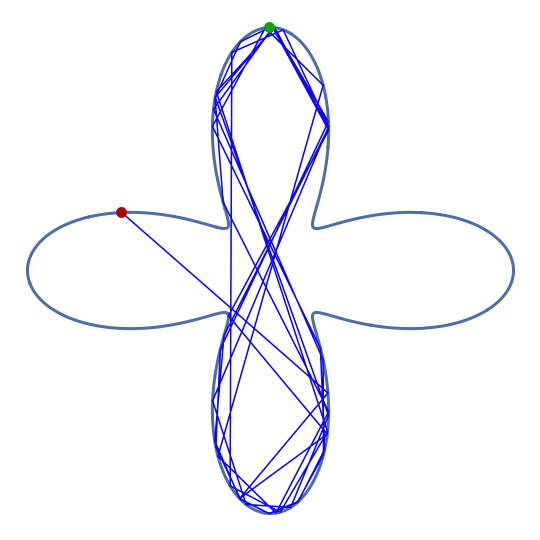But there's a "pro" version, often called chaotic whispering-gallery modes. You find them in dielectric structures that are deformed away from the ideal circular cross section, and they have been shown to create many interesting new effects with potential application in photonic engineering. In our original work describing the properties of these modes, it seemed inevitable that one important geometric feature of the circular cavity can never be abandoned: its convex shape. Shown on the left is what happens in a non-convex billiard when you try to launch a light ray into a trajectory that grazes the boundary. It turns out to be strictly impossible to maintain a stable whispering-gallery circulation.
This rounded cross shape has four separate regions where the boundary is convex (as seen from the inside), but it also has four corners where the boundary is concave. However, the animation indicates that the ray manages to do something similar to a whispering-gallery motion for a short time, before eventually being deflected into one of the horizontal lobes. The pattern formed by the rays before this happens is reminiscent of a figure eight.
It's not immediately clear that such an ephemeral ray pattern should have a counterpart in the wave solutions for a dielectric optical cavity with the same shape — the long-term behavior of the ray is chaotic and shows no discernible real-space pattern at all. But we decided it's worth investigating this unconventional type of geometry all the same, because if the corresponding modes exist, they could solve an important engineering problem: how to combine the whispering-gallery effect with the controlled input and output of light through waveguides.
This is a question I worked on with my graduate student Kahli Burke.
Isolated whispering-gallery resonators are nice for trapping light over extremely long times, but they're not so great when it comes to making use of this trapped light.
Coupling into and out of the cavity is much easier if we attach waveguides that can carry the light to and from neighboring devices. This is shown in the animation on the left.
But in doing so, you can't help but introduce corners that interrupt the convex shape required for a healthy whispering gallery. The horizontal waveguides in this animation have an exaggerated width to illustrate their disruptive effect. The main message of the wave simulation shown in this movie is: Yes, the figure-eight pattern of the ray model does have a counterpart in the wave solutions! We call these long-lived trapped states of light folded chaotic whispering-gallery modes. Think of these patterns as regular whispering-gallery modes that follow the convex parts of the vertical lobes, but are folded over themselves in the center.
This folded pattern implies that the light intensity is concentrated away from the corners where the waveguides are attached, so the openings have only a small effect on the lifetime of the optical mode. Just like the more "traditional" whispering-gallery modes, our folded version owes some of its optical losses to leakage out of the curved dielectric boundary. This interaction with the environment is actually desirable for sensing applications where you try to detect the presence of chemicals near the boundary by observing the resonant properties of the whispering-gallery mode. In other applications, we'd rather not have this leakage, and instead aim for the longest possible cavity lifetimes. In both cases, the waveguides present an additional leakage pathway.
What our work suggests is that this waveguide leakage is less severe than expected based on the simple ray model, so there's a real chance of having your cake and eating it, too: maintain long cavity lifetimes while also gaining access to the optical modes via conventional waveguides. As is so often the case in engineering, this poses an optimization problem where several tradeoffs must be balanced. For example, what precise shapes maximize the lifetimes for a given number of attached waveguides? Is the additional leakage introduced by waveguide attachments acceptable compared to the radiation losses (especially in the out-of plane direction) incurred when coupling to a convex cavity via an air gap instead?
To address the optimization problem, we need to explore a large parameter space numerically. The wave patterns we're after still have one thing in common with the first animation on this page: they're the quasibound states of the cavity. To find these states for a given geometry and refractive index, we use a boundary-integral code written in Julia, which is publicly available on Github. For a detailed description of the numerics and the phenomena we're interested in, see this publication:
This page © Copyright Jens Uwe Nöckel, 2019-2020
Last modified: Tue Apr 12 17:20:32 PDT 2022
