Microdroplets are of interest in atmospheric science, combustion science and biology. From the optics point of view, they belong to the family of dielectric spheroids.
If you had a crystal ball, it's unlikely that you'd be able to see the future with it. However, if you could see the future, you may well find tiny crystal balls in it.
Microspheres could show up as wavelength-selective devices
in future micro-optical applications. They are already a widely
used tool in quantum optics labs, but their technological
potential is not fully exploited yet.
Shown here is a water droplet falling
vertically while undergoing natural shape oscillations.
We have studied both solid and liquid forms of spheroids. For engineering applications, one can make microspheres from fused silica (glass). A big advantage of silica is that individual resonances can be spectrally resolved with greater easy than in liquids. For basic experimental studies of shape-dependent effects, on the other hand, it may be better to use a material whose shape can be varied more easily. That is one of the advantages of liquid droplets. They can have a wide variety of shapes, and one can moreover make those shapes reproducibly. What we learn from the study of deformed droplets can then potentially be transfered to solid spheroids.
Meanwhile, it has been demonstrated that controllable shape variations in silica spheroids can be achieved. The work done by Scott Lacey and Hailin Wang in this direction has given rise to a collaboration centering on weakly deformed, non-axial spheroids that extends the work described on this page in a new direction.To learn about the scientific significance of microspheres, check out the work of Steve Arnold and the page at the Laboratoire Kastler-Brossel.
Microspheres appeared, e.g., in a special
issue of Science Magazine: "Manipulating coherence"
See the review by Mabuchi and Doherty on page 1372.
New ways of exploiting the strong internal field enhancement within microdroplets are still being discovered: Plasma formation dynamics within a water microdroplet on femtosecond time scales (Courvoisier et alia, Optics Letters February 2003). Some of the optics underlying these short-pulse microcavity experiments is discussed in my recent book chapter with R.K. Chang.
The fascination of marbles and beads comes mostly from the ray-based tricks that light can play in such simple objects. Nature itself presents spectacular effects such as the rainbow as light is caught by the bead-like droplets in a cloud. A wide variety of other phenomena occur in our atmosphere (see also the hexagon page).
In the laboratory, droplets can be produced by squeezing a jet of liquid through a nozzle. Of particular interest to us are ways to make individual droplets of well-defined shape. For that purpose, one uses a vibrating type of nozzle that chops the stream in a periodic way, and then images the falling droplets stroboscopically to catch them reproducibly at a predetermined stage of their shape oscillation.
To illustrate why this can be extremely useful for our understanding, let's look at liquid microdroplets more closely.
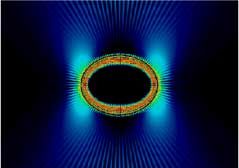Here is a wave calculation for the intensity distribution in
a droplet shaped like a mathematical ellipse. It shows
enhanced light emission near the points of highest curvature,
as one would expect intuitively because of the large "bending"
of the waveguiding walls there.
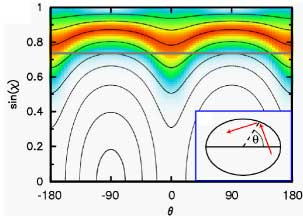The ray-wave connection can be visualized in this surface of section. The black lines are generated
by following a couple of ray trajectories launched within the
cavity, and at each successive encounter with the boundary
recording the polar angle theta along the boundary (see inset).
A two-dimensional plot is generated because we also
record the angle of incidence, chi, with respect to the outward
normal.
The rays inside the ellipse generate continuous curves as shown above. This tells us that there is no chaos in the classical ray dynamics. In color, I have superimposed the wave intensity of the cavity mode shown above. As can be seen from the red band, the wave intensity "condenses" onto the classical structure in this " phase space" spanned by theta and sin(chi).
Here is a wave calculation for the intensity distribution in a
droplet shaped like a quadrupole. As can be seen, the
emission directionality of this cavity is very different from
that of the ellipse, even though the two shapes are quite hard to
tell apart by eye. In particular, the points of globally highest
curvature are located at the same positions in this and the
previous example.
What this implies is that the emission properties can sometimes be very counter-intuitive: light in this case does not emanate tangential to the highest-curvature points, as expected from a naive bending-loss argument.
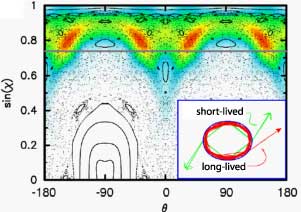The good thing about the ray approach is that it can provide
an explanation for such effetcs. As you can see here, the surface
of section for the quadrupole shows structure that is not present
in the ellipse. The waves see this phase-space structure and form
different patterns as well. This is shown in the color
representation of the wave field. One thing to notice here is
that wave intensity is "pushed away" from the points of highest
curvature (which in this plot lie at theta=0 and 180°), as a
result of some elliptic islands into which the intensity cannot
penetrate.
Microdroplets were one of the first systems in which this
nonintuitive physics was observed experimentally. The details are
to be found in
"Observation of emission from chaotic lasing
modes in deformed microsperes: displacement by the stable orbit
modes ",
S.S.Chang, J.U.Nöckel, R.K.Chang and A.D.Stone, JOSA B
17, 1828 (2000).
PDF.
This page © Copyright Jens Uwe Nöckel, 06/2003
Last modified: Sat Jun 22 09:00:44 PDT 2013
