Repeated Measures ANCOVA

I. Why? To reduce the error variance in experimental designs by accounting for individual differences in responses.

A. Covariates stable over trials. Although random assignment of subjects to conditions theoretically eliminates the possibility of confounding between experimental manipulations and subject characteristics, these individual differences (e.g., IQ, emotional sensitivity) may still affect the subjects’ performance and obscure effects that are present. Hence, experimenters may measure these characteristics and take them into account in analyses of the data.

B. Covariates changing over trials. Subjects may differ in their responses to treatments in ways that can be measured and taken into account in analyses. For example, a researcher investigating the effects of emotion on cognitive processes may induce different emotional states. Because subjects differ in their susceptibility to these inductions, the subjects’ emotional responses may be measured and covaried in analyses of the measures of cognitive processing.

II. How? Different approaches. The linear model approach is described here.

A. Perform a regression treating each observation on each subject as a separate case.

1. Subjects as factors: Each data point can be regarded as a function of the factors including subjects that are used in the analysis. Therefore, subjects could be entered into the model as a factor or as n-1 dummy variables..

2. Criterion scaling: In most real problems there are too many subjects to create n-1 dummy variables. Analyses with this many variables will exceed the capacity of many statistical programs. Fortunately, there is an alternative. Recall that the sums of squares due to subjects represents how the means across conditions for each subject vary around the grand mean. One can take into account the variation due to subjects by creating a variable that is equal to the subject mean on the dependent measure across within-subjects levels. One may then proceed with the analyses, entering this new variable in place of the subject variables.

B. Example without covariate (Winer p. 268; see repeated measures handout)

Drug

Person

Person 1 2 3 4 Mean

1 30 28 16 34 27

2 14 18 10 22 16

3 24 20 18 30 23

4 38 34 20 44 34

5 26 28 14 30 24.5

Drug

Mean 26.4 25.6 15.6 32 24.9

Source SS df MS F

Between S 680.8 4 170.2

Within S 811 15 54.07

Drugs 698.2 3 232.73 24.76

S X D 112.8 12 9.4

Total 1491.8 19

Case Summaries

RESPONSE	SUBJECT	S1	S2	S3	S4	DRUG	LINEAR	QUAD	CUBIC	CRITER
30
1	1	0	0	0	1	-3	-1	-1	108
14
2	0	1	0	0	1	-3	-1	-1	64
24
3	0	0	1	0	1	-3	-1	-1	92
38
4	0	0	0	1	1	-3	-1	-1	136
26
5	0	0	0	0	1	-3	-1	-1	98
28
1	1	0	0	0	2	-1	1	3	108
18
2	0	1	0	0	2	-1	1	3	64
20
3	0	0	1	0	2	-1	1	3	92
34
4	0	0	0	1	2	-1	1	3	136
28
5	0	0	0	0	2	-1	1	3	98
16
1	1	0	0	0	3	1	1	-3	108
10
2	0	1	0	0	3	1	1	-3	64
18
3	0	0	1	0	3	1	1	-3	92
20
4	0	0	0	1	3	1	1	-3	136
14
5	0	0	0	0	3	1	1	-3	98
34
1	1	0	0	0	4	3	-1	1	108
22
2	0	1	0	0	4	3	-1	1	64
30
3	0	0	1	0	4	3	-1	1	92
44
4	0	0	0	1	4	3	-1	1	136
30
5	0	0	0	0	4	3	-1	1	98

Subjects as Factors Regression Design: Dummy variables are created to indicate drug dosage level (here contrast codes were used for Linear, Quadratic, and Cubic polynomials) and subject (here traditional dummy coding was used for S1, S2, S3, S4).

As in the traditional analysis, the total sums of squares can be divided into between and within subjects portions. To obtain the sums of squares for subjects, regress the criterion on dummy variables representing the subjects. To obtain the sums of squares for the within subjects effects, regress the criterion on dummy variables representing the subjects and the within subjects factors. Then subtract the total sums of squares obtained. The difference in the sums of squares is the sums of squares for the added factors.

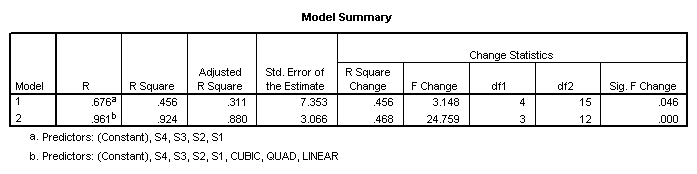
The sums of squares for subjects (680.8) is obtained from the first regression model (which includes only subjects). The residual sums of squares (811) is the within sums of squares. The sums of squares explained in the second regression model (1379.0) represents the sums of squares due to subjects (S1, S2, S3, and S4) and the drug dosage levels (Linear, Quad, Cubic). The difference between these two sums of squares is the sums of squares due to the added factors, i.e., the effect of drug dosage (1379-680.8=698.2). The residual sums of squares from this second model is the sums of squares for the only remaining effect – the subjects by treatment (drug dosage level) interaction. The numbers obtained by this analysis are the same as those given by the traditional analysis (see above).

Criterion scaling Design. To represent the effects of subjects, create a new variable that is the mean (or sum – it differs from the mean only by a constant) of the criterion values for each subject across all of the within subjects conditions. Then regress this variable on the criterion.

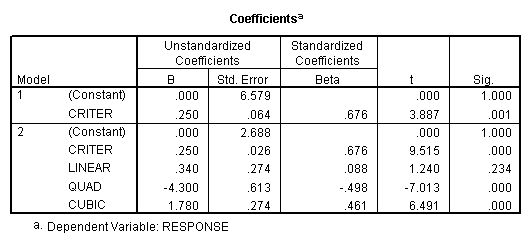
Then proceed as before. The sums of squares for subjects (680.8) is obtained from the first regression model (which includes only subjects). The residual sums of squares (811) is the within sums of squares. The sums of squares explained in the second regression model (1379.0) represents the sums of squares due to subjects (CRITER) and the drug dosage levels (Linear, Quad, Cubic). The difference between these two sums of squares is the sums of squares due to the added factors, i.e., the effect of drug dosage (1379-680.8=698.2). The residual sums of squares from this second model is the sums of squares for the only remaining effect – the subjects by treatment (drug dosage level) interaction. The numbers obtained by this analysis are the same as those given by the traditional analysis and the subjects-as-factors regression (see above). However, the degrees of freedom given in the regression run are wrong because the program treats CRITER as having only 1 degree of freedom when in reality subjects should have n-1 degrees of freedom. So, to obtain the correct mean squares and F ratios, correct the degrees of freedom, calculate the correct mean squares and F tests.

Corrected Statistics:

SOURCE SS DF MS F P

Subjects 680.800 N-1=4 170.2 3.148

Within S 811.000 #Obs-dfS-1=15 54.067

Drugs 811.0-112.8=698.2 C-1=3 232.73 24.76

S X Drugs 112.800 #Obs-dfS-dfC-1=12 9.400

Tests of the trends can also be obtained from the results above by proceeding hierarchically to obtain the requisite sums of squares or by correcting the printed t-tests:

where C=number of conditions

Either of the above approaches can be used with multiple predictors in addition to the dummy variables indicating treatment and/or group membership.

C. Example of ANCOVA using regression approach and criterion scaling (Winer, p. 806)

S^R(A^F) X B^F with one covariate changing over trials.

1. Data

Group	Subject	B1		B2		Total
		X	Y	X	Y	X	Y
A1	1	3	8	4	14	7	22
	2	5	11	9	18	14	29
	3	11	16	14	22	25	38
A2	4	2	6	1	8	3	14
	5	8	12	9	14	17	26
	6	10	9	9	10	19	19
A3	7	7	10	4	10	11	20
	8	8	14	10	18	18	32
	9	9	15	12	22	21	37

2. Analysis.

a. Create new variables

TX=Total X value summed across treatments for one subject.

TY=Total Y value summed across treatments for one subject

b. Perform hierarchical regression treating each observation on each subject for each treatment as a separate case:

Predictors	SS	Residual SS	Terms Added	Change in SS
TX	178.371	196.129	TX	178.371
A+TX	232.630	141.870	A	54.259
A+TX+TY	277.000	97.5	TY	44.37
A+TX+TY+X	339.745	34.755	X	62.475
A+TX+TY+X+B	369.163	5.337	B	29.418
A+TX+TY+X+B+A*B	371.502	2.998	A*B	2.339

c. Use sums of squares obtained from this analysis in constructing a traditional MS table:

Source	SS	df	MS	F
Average X	178.371	1
A	54.259	2	27.13	3.06
S(A)	44.37	6-1	8.87
X	62.475	1
B	29.418	1	29.418	49.03
A*B	2.339	2	1.16	1.93
S(A)B	2.998	6-1	0.600

d. Note that the results obtained using this method may differ slightly from those obtained using other approaches. There is some debate over the best approach to repeated measures ANCOVA.

e. With a covariate that does not change over trials, the same steps may be followed -- omitting the “X” variable of course!