Multiple Regression

I. Why multiple regression?

A. To reduce stochastic error, i.e. increase ability to predict Y

B. To remove bias in estimates of b.

C. Note there are two goals of MR: prediction and explanation - involve different strategies.

II. Two Independent variables

A. Regression Equation.

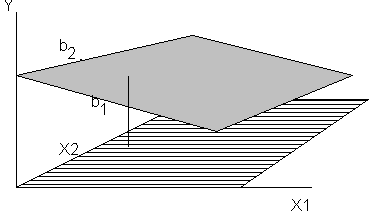
Just as simple linear regression defines a line in the (x,y) plane, the two variable multiple linear regression model Y = a + b₁x₁ + b₂x₂ + e is the equation of a plane in the (x₁, x₂, Y) space. In this model, b₁ is slope of the plane in the (x₁, Y) plane and b₂ is slope of the plane in the (x₂, Y) plane.

B. Regression coefficients

1. Unstandardized

The b_i's are least squares estimates chosen to minimize

=

To find the formulae for these estimates, transform the x_i as before and take the first derivatives with respect to a, b₁, and b₂ and set each equal to 0. This yields the system of equations:

a =

Sx_1iy_i = b₁Sx_1i² + b₂Sx_1ix_2i (1)

Sx_2iy_i = b₂Sx_2i² + b₁Sx_1ix_2i (2)

rearranging equation (1) to solve for b1 yields:

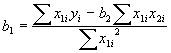
Thus, b₁ depends on b₂ and the covariance between x₁ and x₂.

2. Standardized.

a. The relation between b₁ and b₂ is easier to see if standardized regression coefficients are used; i.e. coefficients from a regression of standardized variables onto a standardized variable:

Z_y = b_z1z₁ + b_z2z₂ Note: b_i = b_zi s_y/s_i

This means that the regression coefficient of Z₁ is the correlation of Z₁ with y minus the correlation of Z₂ with y to the degree that Z₁ and Z₂ are correlated, divided by the variance in Z₁ not "explainable" by (i.e. not overlapping with) Z₂.

Note: when r₁₂ = 0 then b_zi = r_yi

b. Interpretation of standardized b's.

1. Standardization merely scales all variables to the same scale by dividing each score by its variance (after subtracting the variable's mean).

2. If variance in the variable is meaningful (i.e. it is not just a function of the measurement techniques), one may not want to perform this transformation.

3. Standardized b's are sometimes used as indicators of the relative importance of the x_i's. However, "importance" is likely to be related to the ease with which a change in position on a predictor is accomplished in addition to the size of the effect of that predictor on the criterion.

4. Note also that standardized regression coefficients are affected by sample variances and covariances. One cannot compare b_z's across samples.

3. Comparison of b and b_z (from Pedhazur)

	Sample 1				Sample 2
		x1	x2	y		x1	x2	y
Correlations	x1	1			x1	1
	x2	0.5	1		x2	0.4	1
	y	0.8	.7	1	y	0.6	.45	1
sd		10	15	20		8	5	16
Mean		50	50	100		50	50	100

Samples 1 and 2 have the same ranking of r's and the same means and the same regression equation: Y = 10 + 1.0x₁ + .8x₂ . However, the b_zi differ considerably!

Recall that b_zi = b_i(s_i/s_y)

Sample 1 Sample 2

b_z1 1(15/20) = . 5 1(8/16) = .50

b_z2 .8(10/20) = .6 .8(5/16) = .25

C. Regression Statistics

1. Model Statistics

a. Proportion of variance explained

R² = SS_regression/SS_total

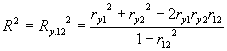
Note: when r₁₂ =0, then R_y.12² = r_y1² + r_y2²

R_y.12² is the R² obtained from a regression of y on x1 and x2; this notation is useful when discussing several different regression models that use the same variables.

b. Adjusted R²

R² is dependent on the sample size and number of independent variables. For example, when N = 2 and k = 1 a perfect prediction of every data point can be made. A regression on these data will yield a line joining the two points. In this case R² = 1. The expected value of the estimated R² = k/(N-1) when the true R² = 0. Thus when k is large relative to N, the estimated R² is not a good estimate of the true R². In replications of the study, the R² obtained is expected to be smaller. To adjust the estimated R² one can use the following formula:

= 1 - (1-R²) [(N-1)/(N-k-1)]

Note: for a given number of predictors, the larger the R² and N, the smaller the adjustment. For example (from Pedhazur), for k=3:

		R^2 = .60	R^2 = .36
N	Ratio k/N	Adjusted R^2	Adjusted R^2
15	1:5	.19	.491
90	1:30	.34	.586
150	1:50	.35	.592

Moral: whenever possible have many more observations than predictors.

c. Variance estimate

s² = SS_residual/df_residual = SS_residual/(N-k-1)

where k=number of independent variables.

d. F ratio

F = SS_reg/df_reg dfreg=k

SS_res/df_res dfres=N-k-1

2. Parameter Statistics

a. Standard error of b:

S_by1.2=

b. t-test

t= b₁/S_by1.2

Note: the larger r₁₂ the larger the S_by1.2.

This may result in a significant test of the regression model but nonsignificant tests of the b's. Under these conditions, it is difficult to determine the effects of the x_i's. This is one of the symptoms of multicollinearity.

III. Multiple predictors

A. Mostly extension of two-variable case.

B. Testing significance of a set of variables

i.e., testing the increment in proportion of variance explained (change in R²).

F = SS_fm-SS_rm/df_fm-rm = (R²_y.12..._kfm-R²_y.12..._krm)/(k_fm-k_rm)

SS_res(fm)/df_res(fm) (1 - R²_y.12..._kfm)/(N - k_fm - 1)

k: number of variables

fm: full model; rm: reduced model

This is useful for testing whether the k_fm - k_rm added variables have an effect over and above effect of the k_rm variables in the reduced model; i.e. whether some sub-set of regression coefficients = 0.

C. Testing the equality of regression coefficients

1. Given Y = a + b₁X₁ + b₂X₂ + ... + b_kX_{k ,} One may wish to test hypothesis that some subset of the true b_i are all equal. To do so, create a new variable W = Sx_i of interest and compare the R² of this reduced model with the original full model as above.

2. Example: test whether b₁ = b₂ in (1) Y = a + b₁X₁ + b₂X₂ + b₃X₃

let W = X₁ + X₂,

then if b₁ = b₂ (2) Y = a + b_wW + b₃X₃

compare R² from model (2) with R² from (1)

3. When comparing only 2 b's, one can use a t-test.

D. Testing constraints on regression coefficients

1. One can use similar methods to test other constraints on the possible values of the b_i's.

2. Example: test whether b₁ + b₃ = 1 in (1) Y = a + b₁X₁ + b₂X₂ + b₃X₃

let b₃=1-b₁

then substituting in (1) Y = a + b₁X₁ + b₂X₂ + (1 - b₁)X₃

Y = a + b₁X₁ + b₂X₂ + X₃ - b₁X₃

Y - X₃ = a + b₁(X₁ - X₃) + b₂X₂

let Y* = Y - X3 and V = X1 - X3

then fit (2) Y* = a + b₁V + b₂X₂

and compare the R² of this reduced model to that of the original full model.

IV. Problems depending on goals of regression models: Prediction

A. One can have several models with adequate fit to the data, to decide which is preferable, one must know what the goal of the study is: prediction or explanation. Multiple regression is used both as a tool for understanding phenomena and for predicting phenomena. Although explanation and prediction are not distinct goals, neither are they identical. The goal of prediction research is usually to arrive at the best prediction possible at the lowest possible cost.

B. Variable Selection

1. Inclusion of irrelevant variables leads to loss of degrees of freedom (a minor problem) and when the irrelevant variables are correlated with included relevant variables, the standard errors of the latter will be larger than they would be without the added irrelevant variables.

2. Omission of relevant variable(s) causes the effect of omitted variable(s) to be included in the error term and when the omitted variable is correlated with the included variable(s), its omission biases the b's of the included variable(s).

a. Example: if the true model is: Y =a + b_y1.2x₁ + b_y2.1x₂ + e

and one fits: Y' = a' + b_y1x₁ + e'

then b_y1 = b_y1.2 + b_y2.1b₂₁

Where b₂₁ is coefficient from regression of x₁ on x₂: x₂ = b₂₁x₁ + e" and b₂₁=r₂₁(s₂/s₁). That is, the estimate of the effect of X₁ on Y is biased by the effect of X₂ on Y to the extent that X₁ and X₂ are correlated.

Note: in multiple independent variable models, the omission of relevant variables may only affect some of the b's greatly. Effect is worrisome to the extent that variables of interest are highly correlated with omitted variable and no other variable that is highly correlated with the omitted variable is included.

3. Selection techniques

a. All possible subsets regression. This is the best (indeed the only good) solution to the problem of empirical variable selection. However, the amount of necessary calculation may be unwieldy, e.g. with 6 independent variables there are:

6 models with 5 variables

15 models with 4 variables

20 models with 3 variables

15 models with 2 variables

6 models with 1 variable

b. Stepwise regression. Two strategies are possible. In forward selection the variable that explains the most variance in the dependent measure is entered into the model first. Then the variable explaining the most of the unexplained variance is entered in next. The process is repeated until no variable explains a significant portion of the remaining unexplained variance. In backward selection, all of the variables are entered into a model. Then the variable that explains the least variance is omitted if its omission does not significantly decrease the variance explained. This process is then repeated until the omission of some variable leads to a significant change in the amount of variance explained. The order of entrance of variables determines which other variables are included in the model.

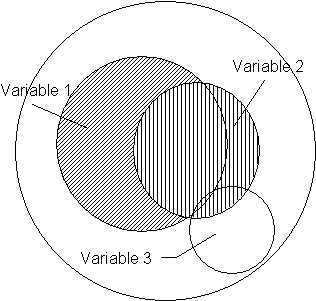
Forward

1. Variable 1 would enter 1st because it explains the most variance in Y.

2. Variable 3 would enter 2nd because it explains the greatest amount of the remaining variance.

3. Variable 2 might not because it explains very little of the remaining variance. Leaving variables 1 and 3 in the equation. However, variable 2 accounts for more variance than 3.

Backward

1. Variable 3 would leave because it explains the least variance. Leaving variables 1 and 2 in the equation.

Moral: Don't do stepwise regression for variable selection. If you do, at least do it several ways.

c. Selection by using uniqueness and communality estimation. Sometimes predictors are selected according to the amount of variance explained by a variable that is explained by no other variable (uniqueness). This technique may be useful for selecting the most efficient set of measures.

V. Problems depending on goals of regression models: Explanation

A. Biggest new problem is multicollinearity: high correlations between predictors. It distorts regression coefficients and may make the entire model unstable and/or inestimable. In simple linear regression, if there is little variance in X, one cannot determine which line through the mean of Y is the best line. This is unimportant if you don't want to predict off of the observed x value. In multiple regression, if the range of some x_i is restricted or the x_i's are multicollinear, one will have multiple possible best planes through the line. It will be impossible to determine which is the "best" line or to isolate the effects of individual variables (since this requires projection off of the line). Regression in these circumstances is very sensitive to outliers and random error.

B. Symptoms of multicollinearity

1. Large changes in the estimated b's when a variable is added or deleted.

2. The algebraic signs of the b's do not conform to expectations (e.g. r with y variable has opposite sign).

3. b's of purportedly important variable have large SE's

C. Detecting multicollinearity

1. Think about variables and check for "high" intercorrelations.

2. Observe correlation matrix.

3. Examine tolerances.

a. Tolerance for x_j is defined as 1-R _xj. _xi.(xj)..xk ²

b. It is a measure of the variance in a predictor that cannot be explained by all of the other variables in the model. It is the 1-R² that would be obtained from a regression on a predictor of all of the other predictors in a model.

c. A tolerance of 1 would be achieved if the predictors are independent. A tolerance of 0 would be obtained if the predictor could be explained by a linear combination of the other predictors.

4. Test determinant of correlation matrix.

a. Calculate |R|. If the matrix is multicollinear, the determinant will be near 0; if its OK, the determinant will be near 1.

b. Find the source of the multicollinearity. Examine R^-1 (if estimable); the diagonals should be near 1. Larger values indicate collinearity; off-diagonal elements should be near 0.

c. Demonstration: when r₁₂ = 1, B = R^-1 r is undefined:

R= |R|=1 - r₁₂²

adj R = R^-1=

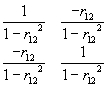
but if r₁₂ = 1, then |R| = 0 and one cannot divide by zero.

When r₁₂ is close to 1, there will be large diagonal elements in the R^-1 matrix. For example, if r₁₂=.96, the minor diagonal elements will be:

-.96 = 12.24

1-(.96)2

D. Remedies for multicollinearity

1. Regression on principal components. Principal components is a technique by which new variables are created by combinations of existing variables so that each PC is independent of all others. However, the b_i's from regressions on PC's may be hard to interpret (but if one is only interested in prediction, this will take care of multicollinearity problems).

2. Create a new variable that is a specified combination of the collinear variables and regress on the new variable. This is a special case of imposing constraints on a model.

e.g. Y = a + b₁X₁ + b₂X₂ + b₃X₃

let W = X₁ + X₂

Y = a + b₁' W + b₃X₃

3. Regress other variables on culprit x_i and use the residuals from this regression as independent variables. (Caution: if there is collinearity in this regression, one may have biased residuals). One may also have trouble interpreting the b_i's produced by this technique.

4. Dump the variable. This will cause misspecification (omitted variable) error i.e., it will bias the estimates of the included variables.