
FIGURE 1. Grey-scale pixel map of explosive probabilities
for a scanned suitcase containing
an elongated piece of C4.
Use of simulated suitcases in refining explosive detection algorithms
G. E. Sieger
Department of Physics, University of Oregon, Eugene, OR 97403, USA
ABSTRACT
From measured transmission of 0.5 - 8.2 MeV neutrons (resolved by time-of-flight) we obtain an elemental analysis (most importantly H, C, N, and O) for each pixel through a sample. A simulated suitcase, which can be analyzed in a similar way, is set up as a 3D array of packing cells. Regions of connected cells are generated by random accretion around seed cells. Each region is then filled with an item selected randomly from one of three lists, according to the size of the region. A typical suitcase contains about 50 items and about 10 per cent empty space. In each explosive suitcase a specified region of variable size and shape is reserved for one of several types of explosive. The elemental composition of each pixel corresponds to a likelihood of containing explosive, obtained from more than a billion simulations of individual pixels. This likelihood is a true probability only in the context of the assumed sample population. The pixel likelihoods for each suitcase are stored in a data base of explosive and non-explosive suitcase populations. From these populations a likelihood of a suitcase containing explosive can be found from the number of contiguous pixels exceeding a given likelihood threshold. Finally, an overall suitcase likelihood is calculated by combining the contiguous pixel likelihoods, treated as partially dependent probabilities, for 12 different thresholds.
Keywords: explosives detection, neutrons, spatial correlation
1. NEUTRON SPECTROMETER
A Fast-Neutron Transmission Spectroscopy (FNTS) technique for detecting explosives in airline luggage is currently under development in the Van de Graaff accelerator laboratory at the University of Oregon. Previous publications1,2 and another paper presented at this conference3 describe this technique in some detail. Briefly, an energy continuum of neutrons is produced by bombarding a thick beryllium target with pulsed 4.2-MeV deuterons. Energy-resolved attenuation of 0.5 to 8.2 MeV neutrons is obtained from time-of-flight measurements. A scanned suitcase typically covers about 16 x 20 pixels, where a pixel is 3 cm x 3 cm. Currently suitcases are scanned one slice at a time using a 16-detector linear horizontal array. Attenuations are least-square fitted with total cross sections for H, C, N, and O to determine projected number densities for those elements. A fictitious element X, with an energy-independent cross section of 3 barns, is included in the fit to account for the presence of other elements.
2. EXPLOSIVE PROBABILITIES FOR PIXELS
A pixel measurement is assigned an explosive probability based on its location in a 5-dimensional parameter space. Normalized projected areal densities for H, C, N, O, and X in orthogonal linear combinations provide four of the parameters. Note that one degree of freedom is removed by the constraint that the normalized densities sum to unity. The fifth parameter is the sum of the areal densities (un-normalized) of N and O divided by the average suitcase thickness along the direction of the neutron beam. This ratio, which is a volume density, increases the contrast between luggage items and explosives, since the latter are typically several times denser.
Explosive probabilities are computed from simulations of non-explosive and explosive projections. A non-explosive projection is constructed by choosing items randomly from a luggage list to fill the projection. We have selected 78 different items, some of which are repeated, to make up a list of 184 items. The list contains thirteen synthetic and natural fabrics, which occur either six or twelve times on the list. Six different shoe materials occur twice each on the list. The list also contains books, food, toiletries, medicines, and miscellaneous items (brass, melamine, wood, etc.). The number of items chosen to fill a projection and their respective volume fractions are determined by a randomizing algorithm. On the average about 10 per cent of a projection is left empty. The volume densities of individual items are chosen to include empty space. For example, the density was set at about 0.5 g/cm3 for plastics, about 2.5 g/cm3 for heavy metals, and about 0.13 g/cm3 for fabrics. The average density of a simulated projection is 0.26 g/cm3.
Projected number densities (pnd's) of H, C, N, O, and X for each item in a projection, scaled to the correct volume fraction, are obtained from a table in which 500 sets of pnd's are listed for each item. These pnd's are the result of unfolding simulated neutron spectra with 500 different randomly generated statistical fluctuations for each item. The neutron spectra are inferred from attenuation spectra, which are measured for some items and constructed from measured elemental neutron cross sections and known compositions for the remaining items. The pnd's for individual items are then summed to obtain pnd's for the projection. Initially we followed the more correct procedure of unfolding the neutron spectra for the combined items in each sample projection. However, our current method of unfolding only individual items has reduced the required computation time by about a hundredfold, and the distributions of pnd's obtained from the two methods are not significantly different.
An explosive projection is constructed by adding a randomly selected volume fraction (f) of explosive to a previously constructed non-explosive projection. Equal numbers of samples are generated for six selected explosive types: TNT, RDX, PETN, DATB, TATB, and Tetryl. For TNT the probability density P(f) is zero for f < 0.04, increases linearly up to f = 0.1, and then falls off as (1-f)4. For the other explosives, values of f obtained from sampling P(f) are scaled to smaller fractions in inverse proportion to their estimated explosive power.
The explosive probability space is binned into about 4 million 5-dimensional cells. The numbers of non-explosive and explosive simulations falling in each cell are recorded in a so-called distribution matrix (D-matrix). Our latest D-matrix was generated from about 2 billion sample projections. In principle, the explosive probability assigned to a bin is E/(N+E), where N and E are the fractions of non-explosive and explosive samples, respectively, falling in that bin. Actually, we use an adaptive smoothing algorithm which includes a sufficient number of samples to minimize the combined effects of statistical fluctuations and estimated resolution errors.
Fig. 1 is a grey-scale pixel map of explosive probabilities for a suitcase scanned by our neutron spectrometer. An elongated piece of C4 explosive in this suitcase resulted in seven pixel probabilities >0.99. For pixels in which the projected mass density of H, C, N, and O falls below a threshold value of 1.6 g/cm2 no probability is assigned.

FIGURE 1. Grey-scale pixel map of explosive probabilities
for a scanned suitcase containing
an elongated piece of C4.
3. EXPLOSIVE PROBABILITIES FOR SUITCASES
From the explosive probabilities for individual pixels, how does one assign an explosive probability to the entire suitcase? To date we have scanned about 300 suitcases with our neutron spectrometer, of which about half contained a real or a mock explosive. From the results for about half of these scanned suitcases, a criterion for assigning suitcase probabilities was constructed as follows. For each of twelve pixel-probability thresholds the largest group of contiguous pixels exceeding that threshold is found for a given suitcase. Pixels are contiguous if they are connected either on their sides or diagonally. The probability thresholds we are currently using are 0.996, 0.99, 0.98, 0.95, 0.9, 0.84, 0.77, 0.7, 0.6, 0.5, 0.4, and 0.3. For each score (n = number of contiguous pixels) above a given threshold (t), an explosive probability P(t,n) = E/(E+N) is calculated, where N and E are the fractions of non-explosive and explosive suitcases with score n, after some smoothing.
The rationale for contiguous-pixel tests is that explosives are expected to occur in a single piece or a small number of pieces. A high-threshold test will be most efficient for detecting a compact explosive, whereas a low-threshold test will be best for detecting thin sheets of explosive. We use twelve thresholds in order to anticipate explosives of a variety of sizes and shapes. The probabilities (Pi) for the twelve thresholds are combined to give an overall probability (Pc):
In the above equation m=12 and x=n/m, where n is the effective number of independent tests represented by the twelve threshold tests. We have found empirically that n=1.5 is reasonable choice. Although Pc is not a "real world" explosive probability, it has proven to be a fairly effective ordering parameter.
Large fluctuations are apparent, even after smoothing, in the probability functions P(t,n) derived from real suitcase measurements. This is due primarily to the small number of samples, and also due to the fact that explosive sizes and shapes were not chosen systematically. Consequently, we have developed a program for simulating suitcases, described in the next section.
4. SIMULATING SUITCASES
A suitcase is simulated as a rectangular volume of cubical packing cells. For the results reported here a suitcase is 15x25x10 cells, where a cell is 3 cm on a side. Regions of connected cells, each to be filled with a luggage item, are generated in the following way. In an initially empty suitcase a seed cell is selected at random, and cells are added one at a time, somewhat analogously to crystal growth, to form a region. At each step a cell is randomly picked from among those which share a face with the set of cells already chosen. This cell is added to the set with probability P=exp(-n/n0), where n is the number of cells already chosen and n0 is a constant. If this cell is rejected (with probability 1-P), another surface cell is picked. This process of accretion continues until a size n is reached for which all the surface cells are rejected. The region is then completed. Next, a new seed cell is selected from the remaining empty cells of the suitcase, and the process is repeated to form a second region. The random accretion is weighted to produce regions which are flattened by about a factor of two in the direction of the thinnest dimension of the suitcase. If a completed region is smaller than a specified minimum size, nmin, then it is erased. The process of generating regions continues until no connected set of empty cells is as large as nmin. After some trial and error, values of n0=125 and nmin=6 were chosen. which result in an average of about 50 regions in a suitcase. On the average about 10 per cent of a suitcase remains empty.
The next step is to fill each region with a luggage item. The 78 different luggage items used to fill individual projections (described in Section 2), with some items repeated, are divided into three groups. The largest 25 per cent of the regions in a suitcase, which are sorted by size, are filled with randomly selected items from the first list, which contains only fabrics. The next 30 per cent of the regions are filled from the second list, which contains medium-sized items, such as books and shoe materials. The smallest 45 per cent of the regions are filled from the third list, which contains the remaining luggage items. The distribution of sizes of regions filled from each of the three lists is shown in Fig. 2. This procedure for filling a suitcase has been adjusted so the average composition of a suitcase is nearly the same as that of simulated individual projections. An average suitcase weighs 26.3 kg and has a density of 0.26 g/cm3. An explosive suitcase is constructed from an already packed suitcase by replacing the material inside a specified rectangular volume with a single type of explosive. This volume is not restricted to be a whole number of packing cells.
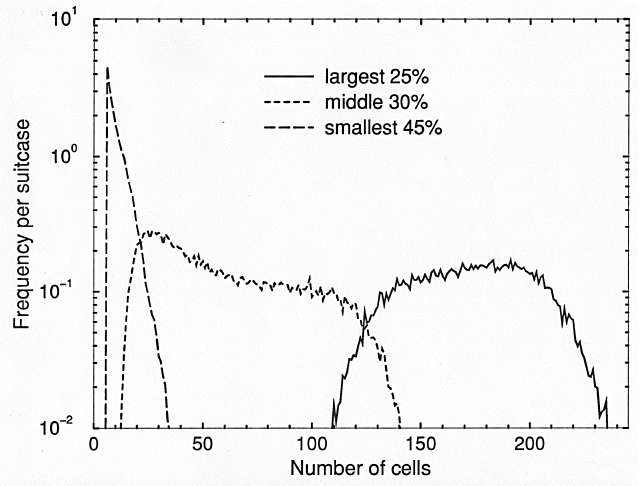
FIGURE 2. Distribution of sizes (number of cells)
of suitcase regions. The three different size groups are filled from
three different luggage lists.
The pixel size was chosen to be the same size as the face of a packing cell. The view through a suitcase is along the thinnest dimension, resulting in a 15x25 pixel array of pnd's and explosive probabilities. Fig. 3 shows that the most likely number of different regions encountered in a projection is four. The number for real suitcases is an important parameter in explosives detection.
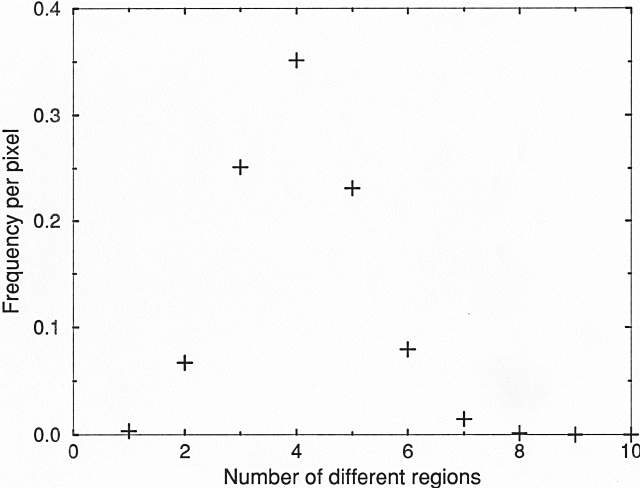
FIGURE 3. Distribution of number of different regions
encountered by projections through the thinnest dimension
of a suitcase.
A problem encountered with real scans is that of "split" pixels, in which different neutron paths through the pixel encounter different materials. For this situation a linear least-squares fit of neutron attenuation is not correct. In our analysis we model a pixel as partially empty, if the fit can be improved by choosing a "fill" fraction of less than one. We have found that this simple modification greatly reduces the inaccuracies due to split pixels in real suitcase scans. In order to include the effects of split pixels in the simulations, the pixel array is shifted diagonally by one fifth of a cell, so that a pixel contains 64 per cent of one cell face and parts of three other cells (or empty space at an edge). Pixels are analyzed as possibly partially empty, as in real scans.
5. RESULTS FROM SIMULATED SUITCASES
In order to obtain suitcase explosive probabilities based on simulations, 9000 non-explosive and an equal number of explosive suitcases were generated. The explosive suitcases were divided equally between two types: TNT and RDX. For each type an equal number of simulations were generated for each of six different shapes. The shapes ranged from 1x8x2 cells (0.71 kg) to 6x10x0.8 cells (2.14 kg) for TNT, and from 1x8x1.2 cells (0.47 kg) to 6x10x0.3 cells for RDX. From these 18,000 suitcases contiguous-pixel probabilities were computed as described in Section 3. The results are shown in Fig. 4.
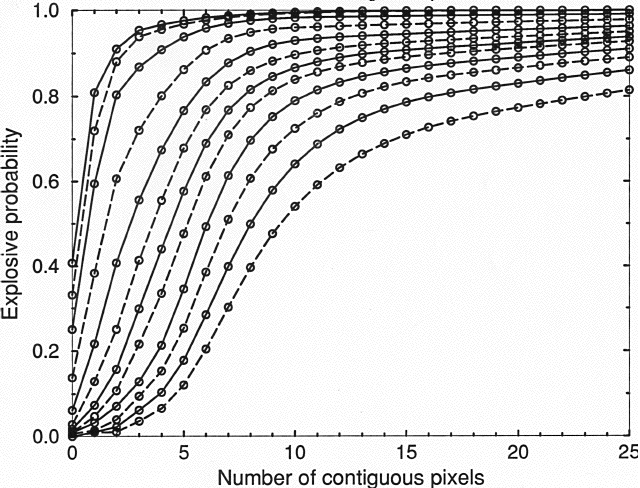
FIGURE 4. Explosive probabilities associated with
groups of contiguous pixels with pixel probabilities above values
of 0.996, 0.99, 0.98, 0.95, 0.9, 0.84, 0.77, 0.7, 0.6, 0.5, 0.4, and 0.3.
The uppermost curve corresponds to the highest
threshold.
As a self-test the discriminant based on the probabilities in Fig. 4 was applied to the 18,000 simulated suitcases. In Figs. 5 and 6 the resulting false-alarm and missed-explosive rates are plotted vs the combined-probability threshold. Even though the explosives were allowed to increase in volume as their thickness decreased, the error rate is greater for thinner explosives. An exception is the 1x8 cell shape, for which no pixel is completely covered by explosive. It can be seen that for explosive thicknesses of 8 per cent of a projection (by volume) of TNT or 3 per cent of RDX result in an overall error rate (for suitably chosen alarm threshold) of about 20 per cent, even though the explosives cover sixty pixels.
When the contiguous-pixel test based on the probabilities of Fig. 4 is applied to the pixel map shown in Fig. 1, a combined explosive probability of 0.964 is obtained. Seven contiguous pixels >0.99 gives the highest individual probability (0.984).
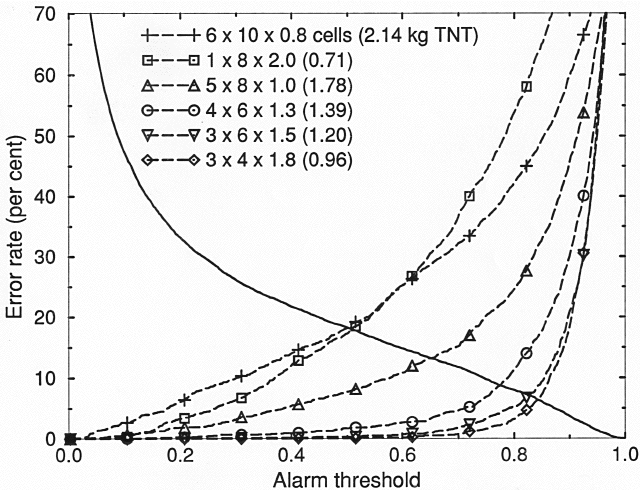
FIGURE 5. False-alarm rate (solid curve) and missed-explosive
rates for six shapes of TNT (dashed curves) versus
combined probability threshold.
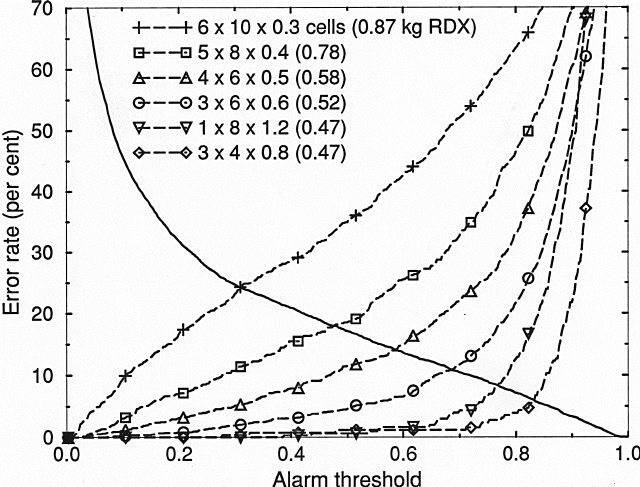
FIGURE 6. False-alarm rate (solid curve) and missed-explosive
rates for six shapes of RDX (dashed curves) versus
combined probability threshold.
6. CONCLUSIONS
We have applied the contiguous-pixel test described in this paper to the suitcases (about 300) we have scanned with our neutron spectrometer. This includes 134 suitcases from a recent FAA-administered blind test, which is described in another paper presented at the present conference4. The fewest number of errors was obtained by setting the alarm threshold at a combined probability of 0.2. Using this test the ordering of suitcases by explosive probability is not significantly different, except for a few cases, from the ordering we would choose after visual inspection of the pixel maps. In cases where our judgement differed from the objective test, we were making use of additional information provided by our analysis, including total projected number densities, goodness of fits (reduced chi-square), and effective Z-values (obtained from ratios of gamma and neutron attenuations5). We are exploring ways of incorporating this extra information into the contiguous-pixel algorithm.
Simulations of FNTS have also been reported6 by a group at Argonne National Laboratory. They have investigated explosives detection based on 3- and 5-view neutron-transmission tomography. Single slices through a suitcase are constructed from randomly placed two-dimensional objects with simple geometrical shapes, such as ellipses and rectangles. In that work discrimination is based on the amount of explosive that could be made from reconstructed number densities of H, C, N, and O.
7. ACKNOWLEDGEMENTS
This work is the result of collaborations with H. W. Lefevre, J. C. Overley, R. J. Rasmussen, R. M. S. Schofield, and M. C. Chmelik. The work was supported by the FAA Technical Center through Grant No. 94-G-020.
8. REFERENCES
1. J. C. Overley, M. S. Chmelik, R. J. Rasmussen, R. M. S. Schofield, and H. W. Lefevre, "Detection of Explosives through Fast-Neutron Time-of-Flight Measurements," Report No. DOT/FAA/CT-94/103, 54 pp, (National Technical Information Center, Springfield VA 22161) 1994.
2. H. W. Lefevre, R. J. Rasmussen, M. S. Chmelik, R. M. S. Schofield, G. E. Sieger, and J. C. Overley, "Using a fast-neutron spectrometer system to candle luggage for hidden explosives," Proceedings of the 5th International Conference on Applications of Nuclear Techniques, Crete, Greece, 1996. To be published by SPIE, The International Society for Optical Engineering.
3. H. W. Lefevre, M. S. Chmelik, R. J. Rasmussen, R. M. S. Schofield, and J. C. Overley, "Using a fast-neutron spectrometer system to candle luggage for hidden explosives. Can it be made practical for first-line airport use?" Proceedings of the present conference.
4. J. C. Overley, M. S. Chmelik, R. J. Rasmussen, G. E. Sieger, R. M. S. Schofield, and H. W. Lefevre, "Results of blind tests for explosives in luggage using fast-neutron transmission spectroscopy (FNTS)," proceedings of the present conference.
5. R. J. Rasmussen, W. S. Fanselow, H. W. Lefevre, M. S. Chmelik, J. C. Overley, A. P. Brown, G. E. Sieger, and R. M. Schofield, "Average Z of Heterogeneous Mixtures from the Ratio of Gamma to Fast-neutron Attenuations," submitted to Nucl. Inst. Methods.
6. C. L. Fink, P. G. Humm, M. M. Martin, and B. J. Micklich, "Evaluation of Few-View Reconstruction Parameters for Illicit Substance Detection using Fast-Neutron Transmission Spectroscopy," IEEE Trans. Nucl. Sci., Vol 43, pp. 1352-1356 (June 1996).