AVERAGE ATOMIC NUMBER OF HETEROGENEOUS MIXTURES FROM THE RATIO OF GAMMA TO FAST-NEUTRON ATTENUATION
R. J. Rasmussen, W. S. Fanselow, H. W. Lefevre, M. S. Chmelik,
J. C. Overley,
A. P. Brown, G. E. Sieger, and R. M. S. Schofield
Department of Physics, University of Oregon, Eugene , Oregon 97403-1274
The attenuation of a continuous spectrum of fast neutrons by each pixel in a luggage image can be used to detect plastic explosives in the presence of other materials. The method involves deconvolution of the attenuations into elemental compositions of H, C, N, O, and X, where X includes everything other than these elements. To improve discrimination, one can also measure the average atomic number, Z, of the mixture of materials in each pixel. We have measured attenuations, by single-element samples, of prompt rays produced from bombardment of a thick Be target with 4.2 MeV deuterons. We report, in this regard, measured prompt gamma-ray spectra, whose median energies indicate that associated attenuations are dominated by Compton scattering. Attenuations were measured subsequently for several thicknesses each of C, Al, Cu, Cd, Sn, and Pb. We have also investigated the attenuation of the fast-neutron spectrum between 8.2 MeV and 5.5 MeV . We found that the ratio of gamma-ray to neutron attenuation generally increases, albeit not linearly, with Z. We apply these results to examine the effective Z of heterogeneous mixtures of H2O-C and C-Al, and have begun to incorporate effective Z into explosives-detection algorithms.
Keywords: neutron attenuation, -ray attenuation, explosives detection,
atomic number
Corresponding author: R. J. Rasmussen, Department of Physics, University
of Oregon, Eugene, OR 97403-1274,
tel: (541) 346-4783, fax: (541) 346-5861, email: rjr@conch.uoregon.edu.
INTRODUCTION
It has been shown that many energetic materials possess distinct chemical signatures, particularly with regards to nitrogen and oxygen content [1]. Various analytical techniques which rely on these characteristics are currently under investigation to determine their efficacy for detecting concealed explosives in airline passenger luggage. We have developed a fast-neutron, time-of-flight (tof), technique for this purpose.
In part, the technique involves unfolding a neutron attenuation spectrum based on individual contributions of the product of the projected number densities, pi, of hydrogen (H), carbon (C), nitrogen (N), and oxygen (O) and their respective total neutron cross sections [2]. All other elemental contributions are lumped together as a fictitious element, X, which has been assigned an energy independent cross section. Based on the results of deconvolution, each picture element, or pixel, of a scanned luggage item addresses a bin in a 5-dimensional, orthogonal, space. The coordinates which span this space are derived from superpositions of particular pi. Through numerous computer simulations, each of the 4x106 bins are assigned a probability, a so-called B-matrix value, that an explosive signature has been encountered. For a complete description of the technique, the reader is referred to the literature [3].
Although the technique has proven very effective, we have found restricting the spectral analysis to 5 basis elements problematic. In particular, when extraneous elements make a substantial energy-dependent contribution to the attenuation spectrum, the unfolding algorithm accounts for such contributions by erroneously adding or subtracting various amounts of H, C, N, and O. These complexities, in principle, can be circumvented by including additional appropriate elements in the analysis. Unfortunately, this approach involves considerably more computing time. At some juncture of the analysis, it would be advantageous to consider an additional parameter to warrant clearly the need to carry out a more complete analysis. We have found that the average atomic number, Z, can serve this purpose. To this end, we have developed a technique to approximate Z of any given material, or assemblage of materials, from the ratio of gamma-ray to fast-neutron attenuation.
EXPERIMENTAL METHODS
Prompt gamma-ray and neutron attenuations were evaluated from neutron tof spectra. Neutrons for these experiments were produced by bombarding a 3mm thick beryllium, Be, target with a 4.2-MeV deuteron beam from the University of Oregon 5-MV Van de Graaff accelerator. The beam was chopped at 1 MHz and klystron bunched; beam duration at the target was about 1.5 ns FWHM. Under these conditions, time-averaged beam currents were approximately 1 microampere.
Neutrons produced at 0o, with respect to the deuteron beam, were collimated to a fan beam by a 40-cm thick collimator of high-density polyethylene. The collimator was sandwiched between 1-m diameter tanks, filled with a water/lithium-carbonate mixture, which served as a target shield. Sixteen neutron detectors, arranged in a linear array, were stationed approximately 4m from the source. Each was constructed from a 6-cm square plastic scintillator, 2.5-cm thick, coupled to a 12-stage Hamamatsu photomultiplier tube, PMT, via a tapered acrylic light pipe.
Timing signals, derived from the deuteron beam and from each PMT, were routed to a time-to-amplitude converter, TAC [4]. Corresponding events were processed by quad analog-to-digital converters, ADCs, and stored as 8192-channel neutron tof spectra in histogramming memories; events were accumulated for typically 80 C of total charge on target. Each raw spectrum was then charge normalized and compressed into standardized 0.2 ns/m flight-time bins. Such spectra exhibit a narrow prompt peak positioned at 3.4 ns/m and several prominent kinematic edges which distinguish various neutron groups characteristic of 9Be(d,n) reactions.
Prompt gamma-ray and neutron attenuations were evaluated from the logarithm of the ratio of background-corrected sample-out (incident) to sample-in (transmitted) standardized spectra over an appropriate flight-time (energy) interval. For gamma rays, a single spectrum channel at 3.4 ns/m was used to evaluate the attenuation, while for neutrons, attenuations were averaged over a relatively high-energy regime (5.5-8.2 MeV) between 25-35 ns/m.
Systematic gamma-ray and neutron attenuation measurements were carried out subsequently for various thicknesses of C, aluminum (Al), copper (Cu), cadmium (Cd), tin (Sn), and lead (Pb). Additionally, attenuations from binary heterogeneous mixtures of H2O-C and C-Al were studied. In each of the cases above, samples were placed directly at the exit slit of the collimator. This provided improved signal to noise by allowing one to average results over several shadowed detectors. For a more complete description of the experimental design, the reader is referred elsewhere [4].
We have also measured the thick-target, 0o, gamma-ray, spectrum from 9Be + d reactions at 4.2 MeV. For these experiments, a 3"x3" NaI (Tl) scintillator was coupled to a PMT, as described above, and positioned in front of the neutron-detector array, about 3.5 m from the source target. In this configuration, the TAC output was coupled to a single-channel analyzer, SCA, which provided a gating signal for an ADC. The linear input signal to the ADC was obtained from the PMT anode after appropriate pulse-shaping amplification. Spectra were then acquired by setting the SCA window on the prompt peak of the neutron tof spectrum. Backgrounds were evaluated by moving the SCA window off the prompt gamma-ray peak.
RESULTS AND DISCUSSION
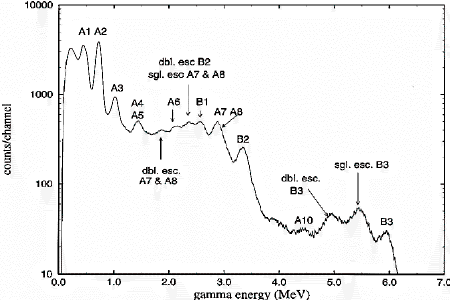
The prompt gamma-ray spectrum observed for 4.2 MeV deuterons on 9Be is shown in Fig. 1. The spectrum has been corrected for background; however, it has not been corrected for the energy dependence of detector efficiency. Most of the prominent peaks have been identified and assigned a label containing the letters A or B. The former are produced from nuclear transitions associated with 9Be(d,n) reactions, and the latter arise from 9Be(d,p) reactions. For a complete description of these peaks, the reader is referred to the relevant literature [5]. As clearly shown, most of the intensity lies between 0.4 MeV and 3.0 MeV. Consequently, interactions involving such radiation should be dominated by the Compton-scattering cross section. For example, Compton scattering in Al dominates other processes between 0.05 - 15 MeV, while for Pb the range is approximately 0.5 - 5 MeV [6]. In light of these findings, we anticipate the absorption, or attenuation, coefficient to depend somewhat linearly on atomic number, Z. A strict linear dependence would be expected for Compton scattering of essentially mono-energetic radiation at energies which preclude contributions from additional scattering mechanisms.

FIGURE 1. Thick-target, zero-degree gamma-ray spectrum
from 9Be + d reactions at 4.2 MeV.
The peaks identified with A labels are associated with 9Be(d,n)
reactions, and those identified with B
labels arise from 9Be(d,p) reactions.
To investigate this prediction, gamma-ray attenuations, denoted ga , were measured for various single-element samples, as described above. Several thicknesses of each sample type were employed to identify potentially influential effects due to beam hardening. Representative data from these experiments are shown for C by the filled circles in Fig. 2, wherein attenuations are plotted against calculated projected number densities, p. For most of the samples investigated, we found ga simply proportional to p. Slightly more complicated behavior, however, was observed for Pb. In this instance, beam hardening and/or additional scattering mechanisms, e.g. Compton plus pair production, were believed responsible. We have, nonetheless, computed an effective attenuation coefficient, dga /dp, for each set of sample data. Subsequent analysis revealed a power-law dependence of the effective attenuation coefficients on Z, i.e. dga/dp Zn, where n=1.25.
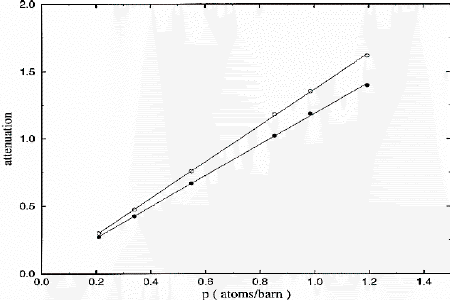
FIGURE 2. Prompt gamma-ray (filled circles) and
fast-neutron (open circles) attenuations for various
projected number densities, i.e. thicknesses, of carbon.
Similar data were obtained for the attenuation of high-energy neutrons; we refer to these attenuations as na. These results are also illustrated in Fig. 2 by the open circles. In slight contrast to the previously mentioned behavior of ga, we found na ~ p for each sample type. Since the na were evaluated at relatively high energy, we expected the corresponding total neutron cross sections, st, to be roughly equal to the geometric cross sections, sg. In this case, sg1/2 depends linearly on A1/3, where A is the atomic mass [7]. Consistently, we found that the values of st, derived from dna /dp, indeed vary with A in this manner. As evidenced below for additional single-element samples, the agreement was less satisfying for light nuclei, where st exhibits considerable resonant structure over the energy interval of interest.
The relationship between st and Z, unfortunately, can be rather complicated. A semi-empirical treatment connects the atomic mass of the most stable nuclei to the corresponding atomic number through the following relation [7]: Z = A / {1.98 + 0.0155 A2/3 }. For light elements, e.g. Z < 20, Z A/2; thus, one again obtains a simple linear relation between st1/2 and, this time, Z1/3. For heavier elements, the full expression for A in terms of Z must be incorporated into the formulation for the geometric cross section. In either case one can express sg as a continuous increasing function of Z.
Based on the above results for ga and na, we define an additional explosives-detection parameter by the ratio of gamma-ray to fast-neutron attenuation. Since both attenuations depend linearly on projected number density, this quantity is independent of sample thickness. Furthermore, to the extent that ga and na are continuous functions of Z , their ratio is also a continuous function of Z, at least over the interval for which Z takes on physically meaningful values.
Thus, we summarize the results of gamma-ray and neutron-attenuation measurements for all sample types and thicknesses in Fig. 3, where values of ga /na are plotted against Z. The attenuation ratios for each sample thickness are depicted by the filled circles, and their corresponding averages are shown by the open circles. The open circle located at the origin was included for line fitting. Note that the deviations in the data increase with Z. Computer-simulation studies indicate these effects result from beam-hardening , manifested by a thickness dependent absorption coefficient for gamma-ray attenuation. For simplicity, we describe the locus of points corresponding to the averaged attenuation ratios by 2 line segments (solid lines) which intersect at Z=6. These line were obtained simply by fitting separately the origin and the averaged carbon point and the carbon point and the averaged lead point.
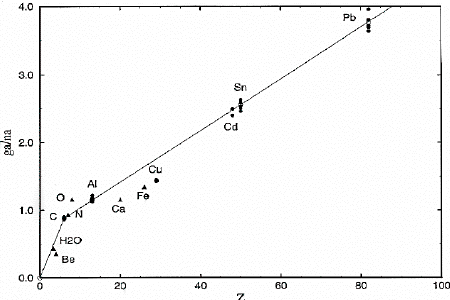
FIGURE 3. Ratio of gamma-ray to fast-neutron attenuations,
ga/na , as a function of atomic number, Z.
The filled circles were obtained from attenuation measurements carried
out on samples of various thick-
nesses, cf. Fig. 2, the open circles are their corresponding averages,
the filled triangles were obtained from
samples of a single thickness, and the solid lines were obtained by fitting
separately the origin with the
averaged C point and the C point with the averaged Pb point.
In order to investigate the usefulness of this approximation, we have measured attenuation ratios for several additional single-element samples, including Be, N, O, calcium (Ca), and iron (Fe). These data are also shown in Fig. 3. For the most part, these data are clustered around the 2 line segments. As mentioned earlier, however, one expects some departure from a smooth Z dependence, particularly for low-Z elements, where the geometric approximation to t is less than adequate. We have investigated this effect further for several additional elements by analyzing total cross-section data obtained from the National Nuclear Data Center at Brookhaven National Laboratory. We averaged their values for t over the same energy interval specified above. We found that the t obtained in this way, generally increased with Z; however, the dependence was not smooth. Although this behavior is presumably also mirrored in the data of Fig. 3, the piece-wise linear approximation shown here was deemed a sufficient measure of Z for our ultimate purposes. Obviously, more sophisticated procedures could be invoked to represent the data more faithfully.
We have applied these results subsequently to investigate the effective Z of various heterogeneous binary mixtures of H20-C and C-Al. Results for the H2O-C series are shown in Fig. 4, where Zeff was obtained from the appropriate line segment of Fig. 3, and <Z> was computed from the number-weighted average for the mixture. As clearly demonstrated by the linear fit to the data, Zeff was essentially equal to <Z> for each mixture. Although nearly identical results were obtained for the C-Al series, we fully expect more complicated behavior from mixtures whose end members do not lie on one of the line segments.
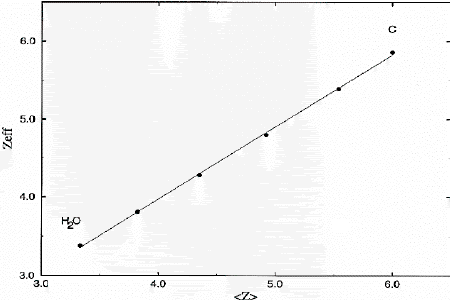
FIGURE 4. Effective Z versus number-weighted average
Z for heterogeneous mixtures of H2O-C.
The solid line is a least-squares fit to the data.
CONCLUSIONS
Notwithstanding, we have begun to incorporate the results of these analyses into an explosives-detection algorithm. In our experience, knowledge of Z greatly facilitates the associated decision process. Firstly, many so-called plastic explosives possess effective Z values which are somewhat larger than ordinary luggage items [8]; consequently, the probability of encountering an explosive is in some way related to Z of the sample in question. Currently, we are evaluating the inclusion of such a probability in a correlation analysis, which yields a single explosive probability from a 2-dimensional array of attenuation spectra corresponding to a given piece of luggage. Finally, Z has proven valuable in revealing various materials which may shield a concealed explosive from the analysis. These situations are almost always conspicuously marked by regions of elevated values of Z. Such cases signal the need to consider additional elemental contributions in the analysis of corresponding attenuation spectra.
ACKNOWLEDGEMENTS
In closing, the authors wish to acknowledge the many supporting efforts of Ms. Barbara Telecky. This work was supported by the Federal Aviation Administration Technical Center under Grant No. 94-G-020.
REFERENCES
1. Fainberg A., Science, 255, 1531-1537 (1992).
2. Overley J. C., Int. J. Appl. Radiat. Isot., 36, 185-191 (1985).
3. Overley J. C., Chmelik M. S., Rasmussen R. J., Sieger G. E., Schofield R. M. S., and Lefevre H. W., "Results of tests for explosives in luggage from fast-neutron time-of-fight transmission measurements", to appear in SPIE Proceedings of the Fifth International Conference on Applicationof Nclear Technologies, 1996.
4. Lefevre H. L., Rasmussen R. J., Chmelik M. S., Schofield R. M. S., Sieger G. E., and Overley J. C., "Using a fast-neutron spectrometer system to candle luggage for hidden explosives", to appear in SPIE Proceedings of the Fifth International Conference on Applications of Nuclear Techniques, 1996.
5. Lauritsen T., and Ajzenberg-Selove F., Nuclear Physics, 78, 1-176, (1966).
6. Segre E., Experimental Nuclear Physics, New York, John Wiley and Sons, 1953, Part II, Section 3.
7. Marmier P. and Sheldon E., Physics of Nuclei and Particles, New York and London, Academic Press, 1969, Chapters 2 and 3.
8. Krauss R. A., Elemental Composition of Explosives, Final Report submitted to the Federal Aviation Technical Center, DOT/FAA/CT-94/20, (1994).