
This page is primarily motivated by our paper, "Goos-Hänchen induced vector eigenmodes in a dome cavity", David H. Foster, J. U. Nöckel and Andrew K. Cook, Opt. Lett. 32, 1764 (2007) (PDF).
My main goal here is to give a basic informal introduction to the phenomenon that forms the basis of our paper. At the time of this writing, this page certainly seems to be more explanatory than the Wikipedia entry. Could I edit the Wikipedia page? Yes, but so could you after reading this page... (at Wikipedia, self-promotion is rightly considered distasteful, though not uncommon; on this page, that rule doesn't apply). There's a more formal discussion of this phenomenon at Scholarpedia.
"Non-specular" reflections refer to deviations from the "ideal" behavior of a mirror, which is to bounce an incoming light beam back in the shape of a V with a well-defined vertex. There has been a recent surge of interest in such effects, and our main contribution was to show for the first time that some unexpected modes in optical cavities can be explained by incorporating Goos-Hänchen shifts into a classical ray model, giving rise to unique bifurcations. We validated this claim in a fully vectorial, three-dimensional solution of Maxwell's equations for a dome cavity with a dielectric mirror. Vectorial field calculations are important for this purpose because reflections at dielectric surfaces are polarization-dependent.
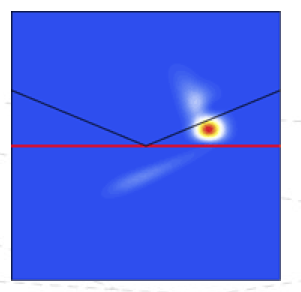
What better way to learn about science than televesion, right? Yes indeed, there is in fact a TV appearance of the Goos-Hänchen effect! So just watch episode 403 of Numb3rs: "Hollywood Homicide" and you'll be educated.
Actually, don't waste your time. The Goos-Hänchen effect in the show is completely bogus. Come to think of it, so is most of the series. "Formulaic Formula Forensics." The image on the right is from a web site called The math behind Numb3rs, where you can glimpse the variety and fun of science without the "middle man" (coincidentally, that page appears to date back to the same year when our paper on the effect appeared – 2007).
The Goos-Hänchen effect is a phenomenon of classical optics in which a light beam reflecting off a surface is spatially shifted as if it had briefly penetrated the surface before bouncing back. The interface has to be between different dielectric materials (such as glass or water), and absorption or transmission should be small enough to allow a recognizable reflected beam to form.
The reason why the show "Numb3rs" is unlikely to have a justifiable need for this effect is simply that the spatial shifts are of order of the wavelength of light (i.e., in the micron range, optimistically). The above image captures part of the physics behind this effect, but it also obscures part of the physics because it doesn't simulate an actual light beam.

There are a couple of ingredients that work together in the Goos-Hänchen effect, and I am going to illustrate this using a movie of electromagnetic wave reflection at a boundary between air (topmost part of the picture) and a material of high refractive index (n = 3.3, as for Gallium Arsenide at a wavelength of 8 μm), occupying the bulk of the image.
The angle of incidence with respect to the vertical is χ = 32°, which in this material is enough to guarantee total internal reflection.
The two-dimensional calculation behind this movie is exact, it does not make the approximation of "Gaussian beams" that is commonly used in laser physics. This way, we can rule out that the Goos-Hänchen effect is an artifact of a misguided approximation or a numerical error.

The animation reminds us that light beams can be described as waves that propagate in a well-defined direction but also have a well-defined width. This makes beams different from plane waves, which form wave fronts of infinite width. For comparison, two nearly plane water waves are shown in the movie on the right. They are very wide, and cross each other at a well-defined angle, forming an interference pattern over a large area (it was Memorial Day weekend, but the lake was virtually undisturbed, thanks to the Oregon climate).
In the total-internal reflection geometry, the incident wave is coming from the bottom left, travels upward inside the material and is ultimately reflected at the surface if χ is large enough. An interference pattern develops only in the small region where the beams overlap. Outside that region, the wave can clearly be called a "beam."
The dielectric-air interface near the top of the image is not a perfect mirror. The wave penetrates into the air and appears to travel parallel to it (from left to right) until the reflection forces it back into the dielectric (heading toward the bottom right).

 Goos-Hänchen shift in total internal reflection.
Specular reflection with phase shifts artificially removed.
Goos-Hänchen shift in total internal reflection.
Specular reflection with phase shifts artificially removed.
Hover over the image to discover the Goos-Hänchen effect. The image represents exactly the same situation as shown in the grayscale movie above, only plotted differently so as to emphasize the highest intensity portions of the beam (essentially, I'm plotting the time averaged energy density of the moving wave pattern on a nonlinear color scale, and this eliminates the wave trains except where they form standing-wave patterns in the region where incident and reflected waves overlap).
When your mouse is over the image, you see the reflection process as it would have been expected to occur without the Goos-Hänchen shift. The red lines forming an inverted V follow the corresponding specular-reflection path without the shift. As your mouse leaves the image, notice how the reflected beam moves over to the right, so the red reference line is no longer in the center of the beam. That's the Goos-Hänchen shift as it occurs in the actual numerical experiment. It's such a small effect that you need this kind of image comparison to appreciate what's going on.
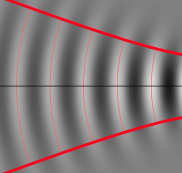
The most common explanation for the Goos-Hänchen shift starts with the observation that spatially confined beams as above can be thought of as superpositions of infinitely extended plane waves. Plane waves reflected by an interface (assumed flat and infinite for our purposes), experience a phase shift which may depend on the angle of incidence, χ. But looking closely at our incident beam, one finds that the plane waves from which it is constructed don't all have the same value of χ. The more focused we want our beam to be, the larger the range of χ for the required plane-wave components. You can see this in the first movie, and in the image on the left: the beams fan out slightly as they recede from the focus, and their wave fronts are curved like segmens of concentric circles.
The shape of the beam transverse to its propagation direction depends on the amplitude and phase with which the plane-wave components are superimposed. So if the phases of different plane waves are shifted differently upon reflection, the transverse shape of the reflected beam will be modified. Measuring the intensity maximum of this reflected beam, one then observes a transverse displacement.
The size of the shift can only be obtained from a wave calculation. This becomes even more important when the reflecting interface is not between a homogeneous dielectric and empty space. The Goos-Hänchen effect can also be observed when the "outer" medium is a more complex, structured material. Most high-quality mirrors in optics are in fact of the latter type: they are made of multiple alternating layers with thickness smaller than the wavelength (i.e., they require nano-scale fabrication), and their reflectivity is based purely on interference, which is of course a wave phenomenon. The work to be described below and in [4] relies on such mirrors.
No matter what the reflection mechanism is (total internal reflection or nanostructured materials), a calculation of the Goos-Hänchen shift always starts by calculating the plane-wave reflection phase shifts as a function of χ, the way I described it above. In the simplest analytical treatments, that's all you need to know — it doesn't even matter what the precise shape of the incident beam is.
The displacement of the reflected intensity pattern due to reflection phase shifts can be re-interpreted when talking about the scattering process in the ray picture, because the resulting beam shape allows us to define a reflected ray. Essentially, rays can be understood as fictitious particles that are pushed forward by the wave fronts like surfers riding toward the beach.
The moral of the story: don't believe anything you see on TV or on the internet...
The Goos-Hänchen shift is the oldest confirmed example of a whole class of so-called non-specular effects. Some argue that it dates back to 1718, because Isaac Newton speculated (no pun intended) about the possibility of non-specular deflection of light in his famous work, "Opticks, or, A Treatise of the Reflections, Refractions, Inflections and Colours of Light." This story is told for example in Physics World — but I cannot find any evidence that it's true. What Newton actually said goes in a rather different direction:
Query 4. Do not the Rays of Light which fall upon Bodies, and are reflected or refracted, begin to bend before they arrive at the bodies; and are they not reflected, refracted, and inflected, by one and the same Principle, acting variously in various Circumstances?
This should be viewed in the context of Query 1 in which Newton speculates whether light rays can be bent by objects "at a distance:" He proposes a non-specular effect based on forces experienced by the corpuscles of light, much like what we now know gravity is capable of doing (and Newton's theory does indeed predict that light is deflected by stars, albeit by half as much as what was later calculated from Einstein's general theory of relativity)! But unfortunately for Newton, corpuscles of light turned out not to be able to explain all optical phenomena.
Clearly it's not justified to say that the Goos-Hänchen was predicted by Newton, because it's a wave effect. However, we do know that Newton's ideas about light are by no means obsolete:
When we speak of "fictitious particles," you should keep in mind that there is a duality between wave and particle description of light, and the particles of light (photons) can manifest themselves in very real ways if we decide to measure them. Conversely, what we learn here about light waves is equally applicable to quantum particles, because all of them can also act like waves. The Physics World story linked above is a case in point, reporting on the Goos-Hänchen effect in neutron scattering.
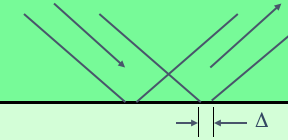
The ray representation of the lateral shift is illustrated in the figure on the right.
It is possible to think about the lateral shift as resulting from from a penetration of the beam into the outside medium. But what determines the "penetration depth" of the ray? The answer is, as we noted above, that it's a wave phenomenon and hence outside the scope of ray physics. That's why we didn't draw this penetrating ray in the adjacent picture. This emphasizes the fact that the Goos-Hänchen shift is not the same as the classical-mechanics problem of a particle reflected by a smooth potential-energy gradient: our shift produces a discontinuity in the ray trajectory which isn't governed by a potential energy (in the sense of classical mechanics).
In such a seemingly pathological situation it's especially interesting to ask what the relation between the ray and wave description of the system looks like. Many standard optical setups (in particular when Gaussian beams are involved) can be described fully by identifying one or a few rays, and decorating them with suitable wave patterns (i.e., phase information) in well-known ways.
When rays form families with well-defined caustics, one can often describe the wave solution succesfully using the WKB approximation or a generalization of it, the Einstein-Brillouin-Keller method. The simplest illustration is the plane wave, which corresponds to an infinitely extended bundle of parallel rays. When such a treatment is possible, it is often unnecessary to look at individual rays in the family, and instead one works with the eikonal which describes the wave fronts to which all the rays must be perpendicular. See examples for the circular dieletric on a separate page. In the eikonal, the scattering phase can be incorporated as just one of several contributions to the phase that accumulates as the wave fronts evolve.
The importance of individual rays increases drastically in systems where the WKB method breaks down, because that corresponds to the scenario where ray chaos may appear. In chaotic dynamics, new periodic ray patterns can form by bifurcation of existing simpler orbits.
So there are situations where isolated ray trajectories are needed to describe the wave patterns. An important type of wave that can be put into correspondence with an isolated ray is the (fundamental) Gaussian beam. It is for this type of wave that the Goos-Hänchen effect was first described.
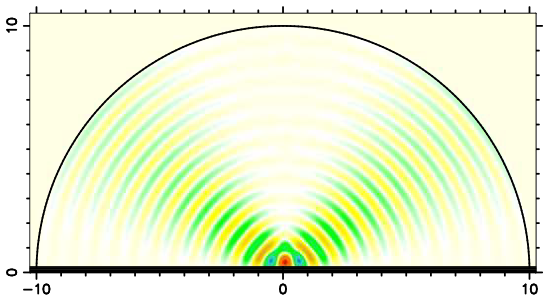
I first learned about the relevance of the Goos-Hänchen effect in dielectric microresonators from Richard Chang and Dipak Chowdhury [1]. This was in the mid-nineties, and in these resonators (see image on the right) I was observing reasonable agreement between the lifetimes of quasibound states from my numerical wave calculations, and a ray model in which I had incorporated curvature-corrected Fresnel reflectivity formulas. So initially, I decided not to look for additional corrections due to the Goos-Hänchen shift because it didn't seem quantitatively necessary.
However, the Goos-Hänchen shift has a strange fascination, so I decided to explore it some more with Martina Hentschel at the Max-Planck Institute for Physics of Complex Systems in Dresden [2]. One motivation came from an apparently boring test case that I originally only studied to validate my numerical computations of quasibound states: the mathematical ellipse (see figure), for which the wave equation can be "solved by hand" under Dirichlet boundary conditions, i.e., if its perimeter were an ideal mirror. One says that the Dirichlet problem in the ellipse is integrable. This means in particular that the internal dynamics of the ellipse should not display any traces of chaotic ray orbits. An ellipse is a very particular type of oval: there are many ovals (e.g., the egg!) which aren't ellipses. Compared to general ovals of identical eccentricity, it is typically a good approximation to consider the dielectric ellipse as non-chaotic, as can be seen on this page discussing dynamical eclipsing.
It is a known fact that resonator shapes that would be integrable for Dirichlet boundary conditions generally do not retain that property in their wave equation when they are made of dielectric material. This is true not only for the ellipse, but even for the mundane rectangle. Although the interface between an elipse and the surrounding medium coincides with the coordinate lines of the elliptic cylinder coordinate system, the wave field on the boundary cannot be assumed to have a constant value (or constant derivatives, for that matter). The reason is that the light will attempt to leak out preferentially near spots of highest curvature, and the curvature is not constant unless the ellipse degenerates to a circle. Some visualizations of how light penetrates the surface of a circular dielectric are shown on a spearate page.
It is this penetration into the interfacial region that underlies the physics of the Goos-Hänchen effect. However, the effect has (for good reason) been studied mostly in the context of planar interfaces, and not curved ones such as ellipses. Although it is also possible to make a convincing argument for the existence of the effect in circular cavities [1], there are some confusing questions that arise when generalizing to shapes like the ellipse.
In [3], we mention the Goos-Hänchen effect as the explanation for the non-separability of the dielectric ellipse. Considering the ray limit of a dielectric cavity, the internal dynamics of the ellipse is strictly integrable when specular reflection at the interface is assumed, whereas the wave equation is not integrable. Could there be a corrected, non-integrable ray dynamics that describes the internal cavity fields better?
The fundamental difficulty with the ray picture is that all waves are plagued by uncertainty relations which make it impossible to simultaneously pin down quantities that are related to each other by Fourier transformation. This is what I was referring to above, when I said that a range of χ is contained in the plane-wave decomposition of a focused beam.
In the ellipse, the spatially varying curvature makes it necessary to specify the position at which a reflection occurs, while the Goos-Hänchen shift depends on the incident beam's direction of propagation. This incident angle cannot be pinned down simultaneously with the position, but that's just what has to be done in the ray picture. As a result, reliable analytical formulas for the shift in the presence of curved interfaces have so far not been derived.
There is by definition not a lot of room in a microcavity, but one can, so to speak, make more room by shrinking the wavelength in comparison to the cavity dimensions. In this semiclassical limit, the uncertainty relations become less uncertain, and the ray picture becomes more accurate. Then it becomes possible to observe the Goos-Hänchen shift in new ways that are peculiar to the resonator scenario. In contrast to free-space experiments with incident and reflected beams, we can for example look for the resonance frequencies at which certain modes appear.
This is what's depicted in the figure above.
As we proved in [4], the Goos-Hänchen shift does indeed manifest itself in the spectra and wave functions of cavities with dielectric boundary conditions. The geometry we considered is nearly integrable, and in that sense it is similar to the example of the ellipse. However, we did the calculations for a three-dimensional dome. The dome is a hemispherical shell whose height is just slightly shorter than its radius. This acts as an ideal curved mirror, and the cavity is closed off by a planar, dielectric multilayer (Bragg) mirror.
As with the ellipse, this dielectric mirror is partly penetrable. The leakage from the resonator gives all its modes a finite lifetime, but in the context of the Goos-Hächen shift we were more interested in the resonance wavelengths and the spatial mode structure than in the lifetimes. Bragg mirrors are a type of dielectric mirror that can induce reflection phase shifts in a more controllable, engineered way than the simple dielectric boundary shown in the movie earlier.
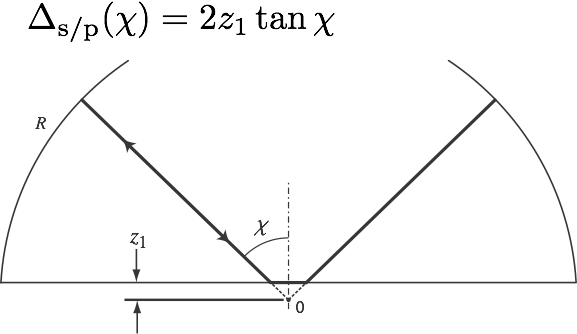
If we now look for the ray on which this wave pattern could be based, we have to draw a gemoetry that includes the shift Δ, as shown on the left. We write Δ(χ) here because the Goos-Hänchen shift depends on the angle of incidence χ, as mentioned earlier.
What follows is a very simple trigonometric calculation that determines the angle of incidence χ of the ray: We know a V-shaped ray must be self-retracing, i.e., hit the dome mirror perpendicularly so as to be reflected back onto itself. The vertex of the V must thus coincide with the center of curvature of the dome, which lies a small distance z1 below the bottom mirror surface. Now the dashed lines around the center 0 describe a right triangle whose catheti are z1 and Δ/2, which leads to the equation above the figure. This can be solved for χ because Δ(χ) is a known function.
Once you have χ, you know the shape and length of the unique stable ray that will support a v-shaped wave pattern in the cavity. Its characteristics (such as the frequencies at which it will appear in the spectrum, and its spot size on the mirror plane) can then be predicted. To re-iterate: if we eliminate the horizontal Goos-Hänchen displacement from our geometric argument, there exists no solution for a v-shaped ray!
The predictions of our Goos-Hänchen-augmented ray model agree very well with numerical simulations of the wave fields, with no adjustable parameters. This shows that resonant modes in optical microcavities can be used to detect the Goos-Hänchen effect. This is a qualitatively new approach to measuring this effect, because it doesn't rely on directly observing the tiny lateral shift of an incident beam. We infer all the properties of the shift from the very presence or absence of individual resonator modes, and their properties — i.e., the opening angle of the V and the wavelength, which is determined by the length of the ray. To find out more about the details of the system, please refer to [4].
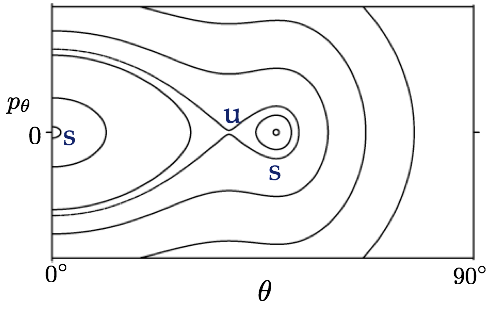
To conclude, it is worth going one step further with a ray-based analysis. The self-retracing orbit just discussed is absent if we switch off the Goos-Hänchen effect (as can be done by replacing the dielectric mirror at the bottom with an ideal metal reflector). It is created by a bifurcation in which a pair of new orbits are "born." But the second member of that pair is a periodic orbit which doesn't correspond to an observed wave pattern. If one new ray orbit creates a new mode, why doesn't the other?
If we really want to understand the wave patterns in our simulations, it is important to analyze the stability of the ray on which the mode is based. This requires looking not just at single orbits but at their neighborhoods. In other words, I end up doing a new type of billiard-ball simulation in which reflections are not specular, but to which the same methods can be applied that are known from our previous work [3].
That's what's shown in the last image. It represents a Poincaré surface of section of the Goos-Hänchen billiard, i.e., a ray billiard where reflections at the dielectric mirror experience the Goos-Hänchen shift. The horizontal axis is the angle of incidence of a ray at the planar mirror, and the vertical axis measures the "rate of change" of that angle between bounces. The labels u, s refer to unstable and stable trajectories. In a Poincaré section, stable trajectories are surrounded by closed (oval) curves that represent rays oscillating around them. The pair u, s in the middle is the one created in the bifurcation mentioned above. But only stable rays can be used to construct transversally confined wave modes of the cavity.
Compared to the dielectric ellipse, our dome cavity simulations are actually much more difficult to do because we're dealing with a 3D structure with mixed boundary conditions, leakiness and polarization-dependent effects. But despite all these real-world complications, the Goos-Hänchen effect lets us say: billards are back! And in the future, other non-specular effects will likely enter the game as well, enriching both the repertoire of billiard physics and our understanding of realistic optical microcavities.
Effect of the Goos-Hänchen shift on the geometrical-optics model for spherical-cavity mode spacingJ. Opt. Soc. Am. A 11: 1110-1116, 1994
2d microcavities: theory and experimentExperimental Methods in the Physical Sciences 40, Academic Press (2002), pp. 185-226
Goos-Hänchen induced vector eigenmodes in a dome cavityOpt. Lett. 32: 1764-1766, 2007
This page © Copyright Jens Uwe Nöckel, 05/2011
Last modified: Sat Nov 17 20:56:42 PST 2012