For an informative description of the historical development of the
Geologic Time Scale and the principles of geology that have been used to
develop it, please visit the Berkeley Museum of Paleontology web page cited
above. I also encourage you to visit the links within the Berkeley page
to learn more about the divisions (Eras, Periods, etc.) of the time scale,
their stratigraphy, life forms and other useful bits of information.
This page is very well done! Students will learn about the principles
of Stratigraphy and application of various relative dating techniques
in the labs devoted to this topic. Lectures will focus on absolute
dating techniques.
| Isotope: | A form of an element whose atoms have the same number of protons and electrons, but a different number of neutrons. |
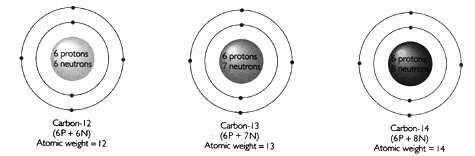
As an example, consider Carbon:
All atoms of Carbon consist of 6 protons and 6 electrons. The different isotopes, C-12, C-13 and C-14 differ in the number of neutrons in the nucleus, and consequently differ in atomic weight. Isotopes are either stable (do not break down spontaneously) or unstable (spontaneously break down, or decay, by nuclear reactions). 98.9% of all Carbon is stable C-12. However, small quantities of radioactive C-14 are produced in the Earth's upper atmosphere by interaction of cosmic rays with nitrogen according to the following reaction:
The resultant C-14 atom quickly combines with oxygen to form CO2. This CO2 may subsequently incorporated into organic matter through the process of photosynthesis:
In radioactive decay reactions, the unstable isotope is referred to as the parent and the element produced by the decay reaction is called the daughter.
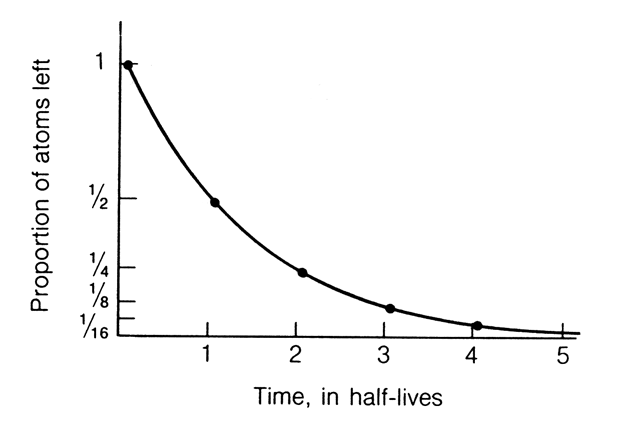For each atom
of a radioactive isotope there is a fixed and constant probability that
it will decay in a fixed period of time. Consequently, at any given
time the % of parent atoms which decay is constant. In other words,
radioactive decay is a Constant Rate Process. The number of
parent atoms that decay in a fixed period of time, or conversely the number
of daughter atoms produced, depends on the number of parent atoms
present at any point in time. Such a relationship results in an exponential
decrease in the number of parent atoms remaining as a function of time,
if "time" is expressed as the half life (the length of time
required for 50% of an initial quantity of radioactive atoms to break down)
. This concept is illustrated in the diagram to the left.
|
|
|
|
| C(14) ==> N(14) | 5,700 years | 2000to- 50,000 years |
| K(40) ==> Ar(40) | 1.3Ga | 100,000 to 4Ga |
| U(238) ==> Pb(206) | 4.5Ga | 100Ma to 4.7Ga |
| Rb(87 ==> Sr(87) | 50Ga | 100Ma to 4.7Ga |
The Radiometric Decay Equation
A constant-rate process such as radioactive decay is described by the simple equation:
where N is the number of radioactive parent atoms present, t is time and l (Greek lamda) is the radioactive decay constant (a number defining the probability that an atom will spontaneously decay in a given time period). In order to use this equation for decay over a given time period, we will need the solution of a first-order differential equation. Obtaining such a solution is beyond the scope and requirements of this class, though with 1-2 years of calculus, you to could do the impossible. The solution is:
The equation above is known as the decay equation. It shows that at any time t, the number of parent atoms, N, is equal to the number of original parent atoms at time zero (N0 gives the number of parent atoms at time zero), multiplied by the natural exponent raised to the negative power of the decay constant (l ) multiplied by the time (t).
Relationship of l to half-life
The decay equation can be used to show the relationship of the decay constant l to the half-life of any unstable isotope. To do this we simply substitute (in the decay equation) t = t1/2 and N = N0/2:
or
Determination of Absolute Ages
The decay equation shown above constitutes the basis for determining
the absolute ages of appropriate rocks and/or minerals. I use the term
"appropriate" in the sense that the specimen to be dated must obviously
contain isotopes of a well known radioactive decay series, and be suitable
for precise chemical analysis. In the simplest ideal situation,the decay
equation is utilized by making the following substitutions:
P = N (# of parent atoms currently present as measured inthe lab)
P0 = N0 (# of original parents at time zero) Note that this is an unknown
D = P0 - P (# of daughter atoms present as measured inthe lab)
If we assume for the moment (more on this later) that no daughters were present at time zero, then:
P0 =P + D and:
or
We can now rearrange this equation to solve for t as follows:
Therefore, if we know the decay constant (l) and can accurately measure D and P, in principle, we can determine the absolute age.
Accurate measurement of either the absolute or relative abundance of
trace quantities of radioactive isotopes requires sophisticated instruments,
known as mass spectrometers, and instrument operators who really
know what they are doing. The technique appears to be simple and straightforward,
but is actually very difficult and time-consuming. Depending on the system
and the specimens, reliable age determinations can take months to be made
and can cost up to $1,000. It is not a trivial task!
Starting the Radiometric Clocks
1. Carbon-14 Dating: Living organisms continually exchange carbon with the atmosphere through the process of photosynthesis. When the organism dies, however, exchange of carbon ceases and the carbon present in the organism becomes isolated. This event (death of the organism) marks the effective starting of the C(14) clock. One of the most common types of material used in C(14) dating is charcoal (e.g., trees burned during a volcanic eruption).
2. Igneous Rocks: These rocks form by the cooling and crystallization of hot silicate liquids (magma or lava). As cooling proceeds from high temperatures (ca. 1100 to 600 degrees C), minerals grow. A growing mineral may trap small amounts of a radioactive isotope within its crystal structure. When this occurs, the radioactive atoms become effectively isolated or trapped. Subsequent disintegration will produce daughter atoms replacing the original radioactive parents. Consequently, the process of cooling and crystallization starts the clock for igneous rocks. In many respects, igneous rocks are the easiest to date because the starting of the clocks are unambiguous.
3. Sedimentary Rocks: Sedimentary rocks are, to a large degree, made from fragments of pre-existing rocks that have been broken, weathered, transported and ultimately deposited in ocean basins. These fragments (e.g., sand or mud) may become cemented together to form sedimentary rocks. The original source for the sediment may have been diverse, consisting of different rock types of different ages. Consequently, a sedimentary rock such as a sandstone or a shale is likely to consist of framgents of different age. Radiometric dating of sedimentary rocks is, therefore, not common.
4. Metamorphic Rocks: These rocks typically form
in deep levels of the crust, and consist of minerals that have formed in
response to increasing temperature and pressure. If a new mineral
grows in a metamorphic rock, and if that mineral incorporates radioactive
isotopes in its crystal structure, then dating of that mineral can provide
an estimate of the time of mineral growth (metamorphism). Most metamorphic
rocks are very complex, and many have undergone several episodes of metamorphism
and/or mineral growth over protracted periods of time. Radiometric
dating of metamorphic rocks can be successful, but often the results are
difficult to interpret, and in many cases are ambiguous.
The Problem of Initial Parent/Daughter Ratios
The simplified application of the decay equation presented above, bases age determinations on measurement of the ratio of parent : daughter isotopes. The fundamental assumption in this simplified approach is that there existed no daughter atoms at the time the radiometric clock started. This assumption is in many cases not valid, as daughter atoms certainly existed in the mineral or rock at the time the radiometric clock started. The solution to this problem can be illustrated using the Rubiduim (Rb) - Strontium (Sr) system.
Rubidium exists as stable Rb(85) and unstable Rb(87). Rb(87) decays to Sr(87) by beta decay (same as C(14)), with a half-life of 50Ga. Strontium has four isotopes [Sr(84), Sr(86), Sr(87) and Sr(88)]. Sr(87) in a given rock may have been produced by the decay of Rb(87) or it may have been present initially as part of the total Sr incorporated before any radioactive decay.
With Sr(87) as the daughter and RB(87) as the parent, the decay equation presented above is:
Sr(87) = Rb(87) (e-lt - 1)
If some Sr(87) was initially present, the total amount of Sr(87) present is given by the following:
Sr(87) total = Sr(87) initial + Rb(87) (e-lt - 1)
The solution around the problem can be attained by using ratios, instead of absolute abundance:
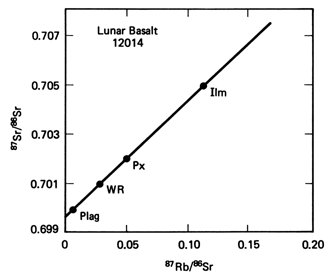The figure to the
left shows such an example of using the ratios of Sr(87)/Sr(86) and Rb(87)/Sr(86).
The rock dated is from the Apollo Lunar mission, as is a basalt from a
Mare basin. Three minerals were analyzed - ilmenite (Ilm), pyroxene
(Px) and plagioclase feldspar (Plag). In addition the whole
rock (WR) was analyzed. All four point fall on a straight line known
as an isochron (meaning same age). The intercept on the Y
axis gives the initial ratio of Sr(87)/Sr(86) . The slope of the isochrog
is given by (e^(-lt) -1),
and from this slope the age is determined to be 3.09Ga.
This page created by Jack Rice with Netscape Navigator Gold